题目内容
己知结论“a1,a2∈R+,且a1+a2=1,则
+
≥4:若a1,a2,a3∈R+,且a1+a2+a3=1,则
+
+
≥9”,请猜想若a1,a2…an∈R+,且a1+a2+…an=1,则
+
+…+
≥
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
n2
n2
.分析:根据归纳推理的内容.进行归纳推理
解答:解:因为a1+a2=1,则
+
≥4=22,a1+a2+a3=1,则
+
+
≥9=32,
所以根据归纳推理的定义可知,当若a1,a2…an∈R+,且a1+a2+…an=1,则
+
+…+
≥n2.
故答案为:n2.
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
所以根据归纳推理的定义可知,当若a1,a2…an∈R+,且a1+a2+…an=1,则
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
故答案为:n2.
点评:本题主要考查归纳推理的应用,要求根据几个一般的式子,寻找规律,然后进行归纳猜想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
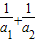 ≥4:若a1,a2,a3∈R+,且a1+a2+a3=1,则
≥4:若a1,a2,a3∈R+,且a1+a2+a3=1,则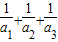 ≥9”,请猜想若a1,a2…an∈R+,且a1+a2+…an=1,则
≥9”,请猜想若a1,a2…an∈R+,且a1+a2+…an=1,则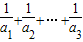 ≥ .
≥ .