题目内容
若方程2(m+1)x2+4mx+3m-2=0的两根同号,则m的取值范围为( )
分析:由题意可得
,解不等式组求得m的取值范围.
|
解答:解:若方程2(m+1)x2+4mx+3m-2=0的两根同号,则有
.
即
,解得-2≤m<-1或
<m≤1,
故选B.
|
即
|
| 2 |
| 3 |
故选B.
点评:本题主要考查一元二次方程根与系数的关系,二次函数的性质的应用,属于中档题.

练习册系列答案
相关题目
 >
>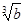 >0”的逆否命题
>0”的逆否命题