Question

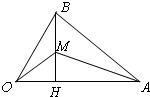（2012•徐汇区一模）如图所示，在△AOB中，∠AOB=

π

3

，OA=3，OB=2，BH⊥OA于H，M为线段BH上的点，且

MO

•

MA

=

5

4

，若

BM

=x

BO

+y

BA

，则x+y的值等于

1

2

．

Answer 1

分析：利用已知条件可以H为原点，HA所在直线为x轴，HB所在直线为y轴，建立直角坐标系，则客气O，A，B的坐标，设M（0，m），则可求向量

MO

，

MA

的坐标，代入

MO

•

MA

=

5

4

可求m，然后由

BM

=x

BO

+y

BA

，可求x+y的值

解答：解：∵∠AOB=

π

3

，OA=3，OB=2，BH⊥OA，
∴OH=1，AH=2，BH=

3

以H为原点，HA所在直线为x轴，HB所在直线为y轴，建立直角坐标系，则O（-1，0），A（2，0），B（0，

3

）
设M（0，m），向量

MO

=（-1，-m），向量

MA

=（2，-m），
∴

MO

•

MA

=-2+m²=

5

4

∴m=

3

2

M（0，

3

2

），
∴

BM

=（0，-

3

2

），

BO

=（-1，-

3

），

BA

=（2，-

3

），
∵

BM

=x

BO

+y

BA

∴（0，-

3

2

）=（-x，-

3

x）+（2y，-

3

y）
∴-x+2y=0，-

3

x-

3

y=-

3

2

所以x+y=

1

2

故答案为：

1

2

点评：本题主要考查了向量的数量积的坐标表示的应用，解题的关键是根据已知条件建立合适的直角坐标系