题目内容
已知椭圆C方程为
，直线
与椭圆C交于A、B两点，点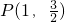
，
（1）求弦AB中点M的轨迹方程；
（2）设直线PA、PB斜率分别为k1、k2，求证：k1+k2为定值．
解：（1）将代入，
消去y并整理得4x2+4mx+4m2-12=0，
△=16m2-16（4m2-12）=48（4-m2）＞0，
-2＜m＜2．
x1+x2=-m，x1x2=m2-3，
，
，
∴弦AB中点M的轨迹方程是
在椭圆内部部分．（6分）
（2）设A（x1，y1）B（x2，y2），A、B两点在直线上
∴
=
（12分）
分析：（1）将代入消去y并整理得4x2+4mx+4m2-12=0，由△＞0，知-2＜m＜2．再由x1+x2=-m，x1x2=m2-3，知弦AB中点M的轨迹方程是在椭圆内部部分．
（2）先设A（x1，y1）B（x2，y2），根据斜率公式即可求出结果．
点评：本题考查直线 与圆锥曲线的位置关系的综合运用，具有一定的难度，解题时要认真审题，合理地进行等价转化．
代入，消去y并整理得4x2+4mx+4m2-12=0，
△=16m2-16（4m2-12）=48（4-m2）＞0，
-2＜m＜2．
x1+x2=-m，x1x2=m2-3，
，，∴弦AB中点M的轨迹方程是
在椭圆内部部分．（6分）（2）设A（x1，y1）B（x2，y2），A、B两点在直线
上∴
=
（12分）分析：（1）将
代入消去y并整理得4x2+4mx+4m2-12=0，由△＞0，知-2＜m＜2．再由x1+x2=-m，x1x2=m2-3，知弦AB中点M的轨迹方程是在椭圆内部部分．（2）先设A（x1，y1）B（x2，y2），根据斜率公式
即可求出结果．点评：本题考查直线 与圆锥曲线的位置关系的综合运用，具有一定的难度，解题时要认真审题，合理地进行等价转化．
练习册系列答案
名校课堂系列答案
相关题目
如图，在平面直坐标系xOy中，已知椭圆
的离心率为
，
：y=x+2与原点为圆心，以椭圆C的短轴长为直
的直线
与椭圆
交于
，
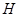两点.设直线
，在
轴上是否存在点
，使得
是以GH为底边的等腰三角形. 如果存在，求出实数
的取值范围，如果不存在，请说明理由.
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．
+
=1，（a＞b＞0）与双曲4x2-
y2=1有相同的焦点，且椭C的离心e=
，又A，B为椭圆的左右顶点，M为椭圆上任一点（异于A，B）．