题目内容
如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,E、F分别为DD1、DB的中点.
(1)求证:EF∥平面ABC1D1;
(2)求证:EF⊥B1C;
(3)求三棱锥 的体积.
的体积.
(1)求证:EF∥平面ABC1D1;
(2)求证:EF⊥B1C;
(3)求三棱锥
 的体积.
的体积.
解:(1)证明:连接BD1,如图,
在△DD1B中,E、F分别为D1D,DB的中点,则
 平面ABC1D1.
平面ABC1D1.
(2)
(3)∵CF⊥平面BDD1B1,
∴CF⊥平面EFB1
且 ,
,
∵ ,
,
 ,
,

∴EF2+B1F2=B1E2
即∠EFB1=90°,
∴ =
= =
=
在△DD1B中,E、F分别为D1D,DB的中点,则
 平面ABC1D1.
平面ABC1D1.(2)

(3)∵CF⊥平面BDD1B1,
∴CF⊥平面EFB1
且
 ,
,∵
 ,
, ,
,
∴EF2+B1F2=B1E2
即∠EFB1=90°,
∴
 =
= =
=

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
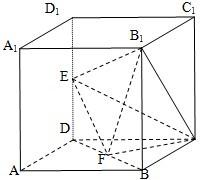 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.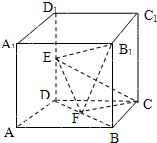 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点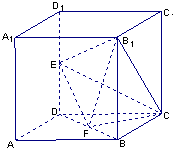 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 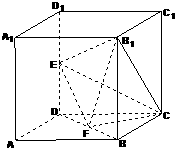 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.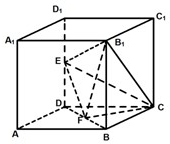 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.