题目内容
奇函数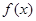 在区间
在区间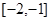 上是减函数,且有最小值
上是减函数,且有最小值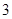 ,那么
,那么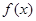 在区间
在区间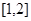 为( )
为( )
A.增函数且最小值为 | B.增函数且最大值为 |
C.减函数且最小值为 | D.减函数且最大值为 |
C
解析考点:奇偶性与单调性的综合.
专题:证明题.
分析:利用奇函数的图象关于原点对称的特点知,奇函数在对称区间上的单调性相同,最值关于原点对称,由此即可正确选择
解答:解:∵函数f(x)为奇函数,
∴函数f(x)的图象关于原点对称
∵函数f(x)在区间[-2,1]上为减函数并有最小值为3,由对称性可知:
则函数f(x)在区间[-1, 2]上为减函数并有最大值-3
故选C
点评:本题考查了奇函数的图象性质,利用对称性判断函数的单调性和最值,关于原点对称的函数的性质

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
下列函数中,在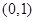 为单调递减的偶函数是
为单调递减的偶函数是
A.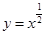 | B.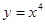 | C.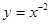 | D.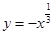 |
设函数 的定义域为A,关于X的不等式
的定义域为A,关于X的不等式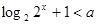 的解集为B,且
的解集为B,且 ,则
,则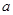 的取值范围是:
的取值范围是:
A. | B. | C. | D. |
设函数f(x)=x|x|+bx+c,给出下列四个命题:
①c=0时,f(x)是奇函数 ②b=0,c>0时,方程f(x)=0只有一个实根
③f(x)的图象关于(0,c)对称 ④方程f(x)=0至多两个实根
其中正确的命题是( )
| A.①④ | B.①③ | C.①②③ | D.①②④ |
已知f(2x+1)是偶函数,则函数f(2x)图像的对称轴为( )
| A.x=1 | B. | C.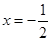 | D.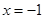 |
函数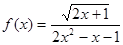 的定义域是( )
的定义域是( )
A. | B. |
C.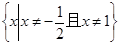 | D.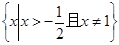 |
(文)函数 的定义域为( )
的定义域为( )
A.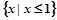 | B.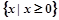 | C.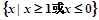 | D.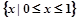 |
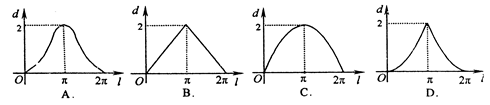
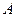 是单位圆上的一定点,动点
是单位圆上的一定点,动点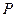 从点
从点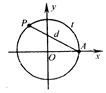
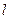 ,弦
,弦 的长为
的长为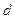 ,则函数
,则函数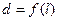 的图像大致是
的图像大致是