题目内容
已知一标准双曲线的两条渐近线方程为y=±2x,则该双曲线的离心率为 .
【答案】分析:因为焦点在x轴上的双曲线的两条渐近线方程为y=± x,焦点在y轴上的双曲线两条渐近线方程为y=±
x,焦点在y轴上的双曲线两条渐近线方程为y=± x,所以分情况讨论a,b的关系,再根据a,b求出c,利用离心率e=
x,所以分情况讨论a,b的关系,再根据a,b求出c,利用离心率e= ,就可求出双曲线的离心率.
,就可求出双曲线的离心率.
解答:解:当双曲线焦点在x轴上时,两条渐近线方程为y=± x,
x,
又∵已知两条渐近线方程为y=±2x,∴ =2,b=2a
=2,b=2a
∴c= a,离心率e=
a,离心率e= =
= =
=
当双曲线焦点在y轴上时,两条渐近线方程为y=± x,
x,
又∵已知两条渐近线方程为y=±2x,∴ =2,a=2b
=2,a=2b
∴c= b,离心率e=
b,离心率e= =
= =
=
故答案为
点评:本题主要考查了双曲线的离心率的求法,关键是求a,c的关系,注意对双曲线的焦点的位置进行讨论.
 x,焦点在y轴上的双曲线两条渐近线方程为y=±
x,焦点在y轴上的双曲线两条渐近线方程为y=± x,所以分情况讨论a,b的关系,再根据a,b求出c,利用离心率e=
x,所以分情况讨论a,b的关系,再根据a,b求出c,利用离心率e= ,就可求出双曲线的离心率.
,就可求出双曲线的离心率.解答:解:当双曲线焦点在x轴上时,两条渐近线方程为y=±
 x,
x,又∵已知两条渐近线方程为y=±2x,∴
 =2,b=2a
=2,b=2a∴c=
 a,离心率e=
a,离心率e= =
= =
=
当双曲线焦点在y轴上时,两条渐近线方程为y=±
 x,
x,又∵已知两条渐近线方程为y=±2x,∴
 =2,a=2b
=2,a=2b∴c=
 b,离心率e=
b,离心率e= =
= =
=
故答案为

点评:本题主要考查了双曲线的离心率的求法,关键是求a,c的关系,注意对双曲线的焦点的位置进行讨论.

练习册系列答案
相关题目
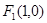 ,
,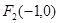 ,直线
,直线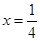 是双曲线的一条准线,
是双曲线的一条准线,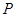 在双曲线右支上,且
在双曲线右支上,且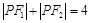 ,求
,求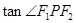 的值。
的值。