题目内容
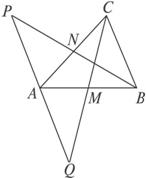
已知△ABC的两边AB、AC的中点分别为M，N，在BN的延长线上取点P，使NP=BN，在CM的延长线上取点Q，使MQ=CM，利用向量证明：P、A、Q三点共线．分析：构造△ABC的两边AB、AC为向量的一组基底，把要证明共线的三点构造两个向量，用基底表示向量，根据是三角形法则，得到两个向量共线，又知两共线向量有公共点，所以三点共线．
解答：解：设
=
，
=
，
∴
=
+
=
+
=
-
，
∴
=
+
=
+
=
-
，
∴
=-
，
∴
∥
，
又因为两个向量有一个公共点A，
∴P、A、Q三点共线．
| AB |
| a |
| AC |
| b |
∴
| AP |
| AN |
| NP |
| AN |
| BN |
| b |
| a |
∴
| AQ |
| AM |
| MQ |
=
| AM |
| CM |
| a |
| b |
∴
| AP |
| AQ |
∴
| AP |
| AQ |
又因为两个向量有一个公共点A，
∴P、A、Q三点共线．
点评：用一组向量来表示一个向量，是以后解题过程中常见到的，向量的加减运算是用向量解决问题的基础，要学好运算，才能用向量解决立体几何问题，三角函数问题，好多问题都是以向量为载体的．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
有两解 B． 
有一解
无解 D． 
有一解