题目内容
(2011•东城区一模)已知函数f(x)=x3+ax2-x+c,且a=f′(
).
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)设函数g(x)=(f(x)-x3)•ex,若函数g(x)在x∈[-3,2]上单调递增,求实数c的取值范围.
| 2 | 3 |
(Ⅰ)求a的值;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)设函数g(x)=(f(x)-x3)•ex,若函数g(x)在x∈[-3,2]上单调递增,求实数c的取值范围.
分析:(Ⅰ)由f(x)=x3+ax2-x+c,得f'(x)=3x2+2ax-1.当x=
时,得a=f ′(
)=3×(
)2+2f ′(
)×(
)-1,由此能求出a的值.
(Ⅱ)因为f(x)=x3-x2-x+c,从而f ′(x)=3x2-2x-1=3(x+
)(x-1),列表讨论,能求出f(x)的单调递增区间和f(x)的单调递减区间.
(Ⅲ)函数g(x)=(f(x)-x3)•ex=(-x2-x+c)•ex,有g'(x)=(-2x-1)ex+(-x2-x+c)ex=(-x2-3x+c-1)ex,
因为函数在区间x∈[-3,2]上单调递增,等价于h(x)=-x2-3x+c-1≥0在x∈[-3,2]上恒成立,由此能求出实数c的取值范围.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
(Ⅱ)因为f(x)=x3-x2-x+c,从而f ′(x)=3x2-2x-1=3(x+
| 1 |
| 3 |
(Ⅲ)函数g(x)=(f(x)-x3)•ex=(-x2-x+c)•ex,有g'(x)=(-2x-1)ex+(-x2-x+c)ex=(-x2-3x+c-1)ex,
因为函数在区间x∈[-3,2]上单调递增,等价于h(x)=-x2-3x+c-1≥0在x∈[-3,2]上恒成立,由此能求出实数c的取值范围.
解答:解:(Ⅰ)由f(x)=x3+ax2-x+c,得f'(x)=3x2+2ax-1.
当x=
时,得a=f ′(
)=3×(
)2+2f ′(
)×(
)-1,
解之,得a=-1.…(4分)
(Ⅱ)因为f(x)=x3-x2-x+c.
从而f ′(x)=3x2-2x-1=3(x+
)(x-1),
由f ′(x)=3x2-2x-1=3(x+
)(x-1)=0,得x1=-
,x2=1,
列表如下:
所以f(x)的单调递增区间是(-∞ , -
)和(1,+∞);
f(x)的单调递减区间是(-
, 1).…(9分)
(Ⅲ)函数g(x)=(f(x)-x3)•ex=(-x2-x+c)•ex,
有g'(x)=(-2x-1)ex+(-x2-x+c)ex=(-x2-3x+c-1)ex,
因为函数在区间x∈[-3,2]上单调递增,
等价于h(x)=-x2-3x+c-1≥0在x∈[-3,2]上恒成立,
只要h(2)≥0,解得c≥11,
所以c的取值范围是c≥11.…(14分)
当x=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解之,得a=-1.…(4分)
(Ⅱ)因为f(x)=x3-x2-x+c.
从而f ′(x)=3x2-2x-1=3(x+
| 1 |
| 3 |
由f ′(x)=3x2-2x-1=3(x+
| 1 |
| 3 |
| 1 |
| 3 |
列表如下:
| x | (-∞,-
|
-
|
(-
|
1 | (1,+∞) | ||||||
| f'(x) | + | 0 | - | 0 | + | ||||||
| f(x) | ↗ | 有极大值 | ↘ | 有极小值 | ↗ |
| 1 |
| 3 |
f(x)的单调递减区间是(-
| 1 |
| 3 |
(Ⅲ)函数g(x)=(f(x)-x3)•ex=(-x2-x+c)•ex,
有g'(x)=(-2x-1)ex+(-x2-x+c)ex=(-x2-3x+c-1)ex,
因为函数在区间x∈[-3,2]上单调递增,
等价于h(x)=-x2-3x+c-1≥0在x∈[-3,2]上恒成立,
只要h(2)≥0,解得c≥11,
所以c的取值范围是c≥11.…(14分)
点评:本题考查参数值的求法和单调区间的求法及求解实数的取值范围,考查运算求解能力,推导论证能力,考查分类讨论思想,转化化归思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
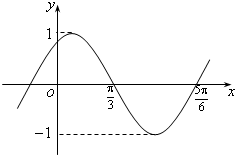 (2011•东城区一模)已知函数y=sin(ωx+φ)
(2011•东城区一模)已知函数y=sin(ωx+φ)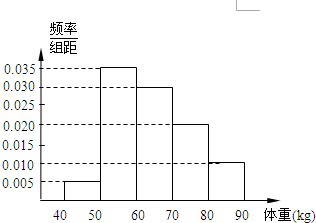 (2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为
(2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为