题目内容
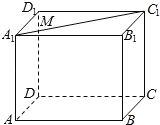
【题目】如图，在正方体
中，若
是线段
上的动点，则下列结论不正确的是( )
A. 三棱锥
的正视图面积是定值
B. 异面直线
，
所成的角可为
C. 异面直线，
所成的角为
D. 直线
与平面
所成的角可为
【答案】D
【解析】
判断主视图的底与高是否发生变化来判断
，利用几何法以及建立空间坐标系将线线角以及线面角的关系转化为向量的关系来判断
，
和
．
对于，三棱锥
的主视图为三角形，底边为
的长，高为正方体的高，故棱锥的主视图面积不变，故正确；
对于，分别以，
，
为坐标轴，以为原点建立空间直角坐标系，设正方体边长为1，
，
，
，
，
∴
，
，∴
，当
时，方程有解， ∴异面直线
，所成的角可为
，故B正确．
对于，连结
，
，
，则
，∵
，∴
，
又∵
，于是
平面
，∵
平面，∴
，故C正确；
对于，结合B中的坐标系，可得面
的法向量为
，
，
所以
，令
，方程无解，即直线
与平面所成的角可为是错误的，故选D.
练习册系列答案
同步练习强化拓展系列答案
相关题目
