题目内容
直线x+y-m=0与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是
- A.1<m<

- B.-
 <m<
<m<
- C.1≤m<

- D.-
 ≤m≤
≤m≤
A
分析:由直线x+y-m=0与圆x2+y2=1在第一象限内有两个不同的交点可得联立方程 可得2x2-2mx+m2-1=0有两个不同的正根,结合方程的根与系数的关系可建立关于m的不等式组,从而可求
可得2x2-2mx+m2-1=0有两个不同的正根,结合方程的根与系数的关系可建立关于m的不等式组,从而可求
解答:∵直线x+y-m=0与圆x2+y2=1在第一象限内有两个不同的交点
∴联立方程 可得2x2-2mx+m2-1=0有两个不同的正根
可得2x2-2mx+m2-1=0有两个不同的正根
∴
∴
∴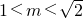
故选A
点评:本题主要考查了直线与圆相交的综合问题.当直线与圆相交时 涉及交点问题时常用“韦达定理法”来解决.
分析:由直线x+y-m=0与圆x2+y2=1在第一象限内有两个不同的交点可得联立方程
 可得2x2-2mx+m2-1=0有两个不同的正根,结合方程的根与系数的关系可建立关于m的不等式组,从而可求
可得2x2-2mx+m2-1=0有两个不同的正根,结合方程的根与系数的关系可建立关于m的不等式组,从而可求解答:∵直线x+y-m=0与圆x2+y2=1在第一象限内有两个不同的交点
∴联立方程
 可得2x2-2mx+m2-1=0有两个不同的正根
可得2x2-2mx+m2-1=0有两个不同的正根∴

∴

∴
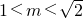
故选A
点评:本题主要考查了直线与圆相交的综合问题.当直线与圆相交时 涉及交点问题时常用“韦达定理法”来解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线x-y+m=0与圆x2+y2+2y-1=0有两个不同交点的一个必要而不充分条件是( )
| A、-3<m<1 | B、-2<m<0 | C、-4<m<2 | D、-2<m<1 |
直线x-y+m=0与圆x2+y2-2x-1=0有两个不同交点的一个充分不必要条件是( )
| A、-3<m<1 | B、-4<m<2 | C、0<m<1 | D、m<1 |