题目内容
(1)已知A={1,x,y},B={x,x2,xy}且A=B,求x、y;(2)设集合P={4,3t+2,5t2},Q={3t-2,5t-6,5t2-1},且P∩Q={4},求实数t及P∪Q.
(1)由集合元素的互异性知x≠y,x≠1,y≠1.
∵A=B,∴x2=1或xy=1.
①x2=1时,取x=-1,此时A={1,-1,y},B={-1,1,-y}.
由A=B,有y=-y,从而y=0.
②xy=1时,即x=![]() ,此时A={1,
,此时A={1, ![]() ,y},B={
,y},B={![]() ,
,![]() ,1}.
,1}.
由A=B,有![]() =y,从而y=1,但与y≠1矛盾,应舍去.
=y,从而y=1,但与y≠1矛盾,应舍去.
综上知x=-1,y=0.
解法二:∵A=B,
∴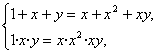
即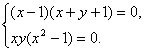
由集合元素的互异性,有x≠1,x≠0.
∴![]()
∴x=-1,y=0.
(2)解:①令3t-2=4,则t=2,此时P={4,8,10},而Q中的元素3t-2,5t-6,皆为4,与元素的互异性矛盾,应舍去t=2.
②令5t-6=4,则t=2,显然不符合要求.
③令5t2-1=4,则t=±1.
当t=1时,集合P中的3t+2与5t2皆为5,与元素的互异性矛盾,应舍去t=1;
当t=-1时,P={4,-1,5},Q={-5,-11,4},满足P∩Q={4}.
综上知t=-1.

练习册系列答案
相关题目
已知
=(1,-2),
=(2,λ),且
与
的夹角为锐角,则实数λ的取值范围是( )
| a |
| b |
| a |
| b |
| A、(-∞,1) |
| B、(0,1) |
| C、(1,+∞) |
| D、(-∞,-4)∪(-4,1) |
 已知an=2n,把数列{an}的各项排成如图三角形状,记A(i,j)表示第i行中第j个数,则结论
已知an=2n,把数列{an}的各项排成如图三角形状,记A(i,j)表示第i行中第j个数,则结论 已知
已知