题目内容
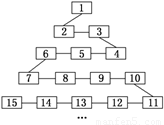
 如图是网络工作者经常用来解释网络动作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第23行从左至右算第4个数字为.
如图是网络工作者经常用来解释网络动作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第23行从左至右算第4个数字为.
- A.275
- B.274
- C.273
- D.272
C
分析:通过观察蛇形模型得到,前n行的数字个数之和刚好等于本行的最大数字,并且奇数行,从大到小排列;偶数行,从小到大排列.所以利用等差数列的求和公式分别求出前98和前99行的最大数字,根据奇数行的规律得到第23行从左至右算第4个数字即可.
解答:前22行一共已出现了1+2+3+…+22= =253个数字,
=253个数字,
前23行一共出现了1+2+3+…+23= =276个数字,
=276个数字,
而第23行的数字从左至右是由大到小出现的,
即依次为276,275,274,273,…,
∴第23行从左至右算第4个数字是273.
故选C.
点评:考查学生掌握等差数列求前n项和的公式,要善于观察,学会归纳总结.
分析:通过观察蛇形模型得到,前n行的数字个数之和刚好等于本行的最大数字,并且奇数行,从大到小排列;偶数行,从小到大排列.所以利用等差数列的求和公式分别求出前98和前99行的最大数字,根据奇数行的规律得到第23行从左至右算第4个数字即可.
解答:前22行一共已出现了1+2+3+…+22=
 =253个数字,
=253个数字,前23行一共出现了1+2+3+…+23=
 =276个数字,
=276个数字,而第23行的数字从左至右是由大到小出现的,
即依次为276,275,274,273,…,
∴第23行从左至右算第4个数字是273.
故选C.
点评:考查学生掌握等差数列求前n项和的公式,要善于观察,学会归纳总结.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
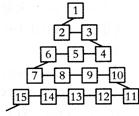 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右算第8个数字为( )
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右算第8个数字为( )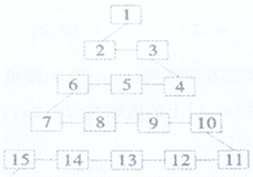 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;以此类推,则
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;以此类推,则 如图是网络工作者经常用来解释网络动作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第23行从左至右算第4个数字为.( )
如图是网络工作者经常用来解释网络动作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第23行从左至右算第4个数字为.( ) 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第5个数应是
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第5个数应是