题目内容
如图，△PAB所在的平面α与四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，则点P在平面α内的轨迹是__________________.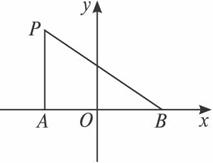
答案：圆的一部分 ∵AD⊥α，BC⊥α，∴AD∥BC且∠CBP=∠DAP=90°.
又∵∠CBP=∠APD，故Rt△CBP∽Rt△DAP，有
.在平面PAB内，以AB所在直线为x轴，AB的中点为坐标原点，建立如上图所示的直角坐标系，则A(-3，0)，B(3，0)，设P(x，y),则
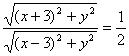，化简得：x2+y2+10x+9=0.注意到点P不在直线AB上，∴点P的轨迹方程为x2+y2+10x+9=0(y≠0)，点P在平面α内的轨迹为圆的一部分.
练习册系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
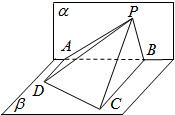如图，△PAB所在的平面α和梯形ABCD所在的平面β互相垂直，且AD⊥α，AD=4，BC=8，AB=6，若tan∠ADP+2tan∠BCP=10，则点P在平面α内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
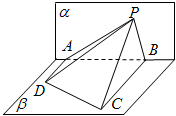如图，△PAB所在的平面α和四边形ABCD所在的平面β互相垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，若tan∠ADP+2tan∠BCP=10，则点P在平面a内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
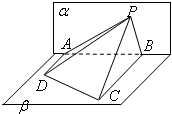如图，△PAB所在的平面α和四边形ABCD所在的平面β垂直，且AD⊥α，BC⊥α，AD=4，BC=8，AB=6，∠APD=∠CPB，则点P在平面α内的轨迹是（ ）| A、圆的一部分 | B、椭圆的一部分 | C、双曲线的一部分 | D、抛物线的一部分 |
，AD=4，
，
内的轨迹是
（ ）