题目内容
经过点(2,0)且与曲线y=
相切的直线方程是
| 1 | x |
x+y-2=0
x+y-2=0
.分析:设切线方程为y=k(x-2),联立直线与曲线方程,利用判别式等于零建立等式,求出k即可,注意验证.
解答:解:设切线方程为y=k(x-2),
所以
即kx2-2kx-1=0
因为相切所以△=4k2+4k=0,解得k=0(舍去)或k=-1,
∴切线方程为x+y-2=0.
故答案为:x+y-2=0
所以
|
因为相切所以△=4k2+4k=0,解得k=0(舍去)或k=-1,
∴切线方程为x+y-2=0.
故答案为:x+y-2=0
点评:本题主要考查了利用判别式求解切线方程,同时考查了转化的思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 相切的直线方程.
相切的直线方程. 曲线相切的直线方程.
曲线相切的直线方程.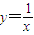 曲线相切的直线方程.
曲线相切的直线方程.