题目内容
.已知椭圆 离心率
离心率 ,焦点到椭圆上的点的最短距离为
,焦点到椭圆上的点的最短距离为 .
.
(1)求椭圆的标准方程.
(2)设直线l:y=kx+1与椭圆交与M,N两点,当 时,求直线l的方程.
时,求直线l的方程.
解:(1)由已知得 ,
,
∵ ,
,
∴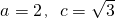
∴椭圆的标准方程为 (6分)
(6分)
(2)设M(x1,y1),N(x2,y2)
由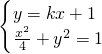 得(4k2+1)x2+8kx=0…(8分)
得(4k2+1)x2+8kx=0…(8分)
△=64k2,
∵直线l:y=kx+1与椭圆交与M,N两点,
∴
∴|MN|=
=
=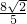 ,
,
∴k=±1,或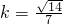 ,(10分)
,(10分)
∴直线方程为y=x+1,或y=-x+1,或y= ,或y=-
,或y=- .(14分)
.(14分)
分析:(1)由已知得 ,
, ,由此能求出椭圆的标准方程.
,由此能求出椭圆的标准方程.
(2)设M(x1,y1),N(x2,y2),由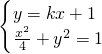 得(4k2+1)x2+8kx=0.再由根的判别式和韦达定理能求出直线l的方程.
得(4k2+1)x2+8kx=0.再由根的判别式和韦达定理能求出直线l的方程.
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点.本题具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 ,
,∵
 ,
,∴
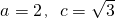
∴椭圆的标准方程为
 (6分)
(6分)(2)设M(x1,y1),N(x2,y2)
由
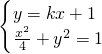 得(4k2+1)x2+8kx=0…(8分)
得(4k2+1)x2+8kx=0…(8分)△=64k2,
∵直线l:y=kx+1与椭圆交与M,N两点,
∴

∴|MN|=

=

=
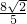 ,
,∴k=±1,或
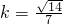 ,(10分)
,(10分)∴直线方程为y=x+1,或y=-x+1,或y=
 ,或y=-
,或y=- .(14分)
.(14分)分析:(1)由已知得
 ,
, ,由此能求出椭圆的标准方程.
,由此能求出椭圆的标准方程.(2)设M(x1,y1),N(x2,y2),由
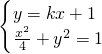 得(4k2+1)x2+8kx=0.再由根的判别式和韦达定理能求出直线l的方程.
得(4k2+1)x2+8kx=0.再由根的判别式和韦达定理能求出直线l的方程.点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点.本题具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C: 已知椭圆C:
已知椭圆C: