题目内容
9.已知数列{an}的前n项和为Sn,满足an=$\frac{{S}_{n}}{n}$+2n-2,n∈N*,且S2=6.(1)求数列{an}的通项公式;
(2)证明:$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$<$\frac{5}{3}$.
分析 (1)利用递推关系、等差数列的通项公式即可得出;
(2)Sn=$\frac{n(1+4n-3)}{2}$=n(2n-1).n≥3,$\frac{1}{{S}_{n}}$=$\frac{1}{n(2n-1)}$$\frac{2}{2n(2n-1)}$<$\frac{1}{2n-3}$-$\frac{1}{2n-1}$.利用“裂项求和”即可得出.
解答 (1)解:∵an=$\frac{{S}_{n}}{n}$+2n-2,n∈N*,且S2=6.
∴a2=$\frac{6}{2}$+2×2-2=5,a1+a2=6,
解得a1=1.
又nan=Sn+2n2-2n,
当n≥2时,(n-1)an-1=Sn-1+2(n-1)2-2(n-1),
相减可得:nan-(n-1)an-1=an+4n-4,
化为an-an-1=4,
∴数列{an}是等差数列,首项为1,公差为4.
∴an=1+4(n-1)=4n-3.
(2)证明:Sn=$\frac{n(1+4n-3)}{2}$=n(2n-1).
∴n≥3,$\frac{1}{{S}_{n}}$=$\frac{1}{n(2n-1)}$$\frac{2}{2n(2n-1)}$<$\frac{1}{2n-3}$-$\frac{1}{2n-1}$.
∴$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$<1+$\frac{1}{3}$+$(\frac{1}{3}-\frac{1}{5})$+$(\frac{1}{5}-\frac{1}{7})$+…+$(\frac{1}{2n-3}-\frac{1}{2n-1})$=$\frac{5}{3}$-$\frac{1}{2n-1}$<$\frac{5}{3}$.
∴$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$<$\frac{5}{3}$.
点评 本题考查了递推关系、等差数列的通项公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.

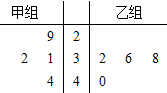 某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.
某商场为推销当地的某种特产进行了一次促销活动,将派出的促销员分成甲、乙两个小组分别在两个不同的场地进行促销,每个小组各4人.以下茎叶图记录了这两个小组成员促销这种特产的件数.