题目内容
若椭圆 和双曲线
和双曲线 有相同的焦点F1、F2,P是两曲线的交点,则|PF1|•|PF2|的值是
有相同的焦点F1、F2,P是两曲线的交点,则|PF1|•|PF2|的值是
- A.

- B.

- C.b-n
- D.a-m
D
分析:利用椭圆、双曲线的定义,结合|PF1|•|PF2|= ,即可得到结论.
,即可得到结论.
解答:∵椭圆 和双曲线
和双曲线 有相同的焦点F1、F2,P是两曲线的交点,
有相同的焦点F1、F2,P是两曲线的交点,
∴|PF1|+|PF2|=2 ,||PF1|-|PF2||=2
,||PF1|-|PF2||=2 ,
,
∴|PF1|•|PF2|= =a-m.
=a-m.
故选D.
点评:本题考查双曲线和椭圆的定义,考查学生的计算能力,属于基础题.
分析:利用椭圆、双曲线的定义,结合|PF1|•|PF2|=
 ,即可得到结论.
,即可得到结论.解答:∵椭圆
 和双曲线
和双曲线 有相同的焦点F1、F2,P是两曲线的交点,
有相同的焦点F1、F2,P是两曲线的交点,∴|PF1|+|PF2|=2
 ,||PF1|-|PF2||=2
,||PF1|-|PF2||=2 ,
,∴|PF1|•|PF2|=
 =a-m.
=a-m.故选D.
点评:本题考查双曲线和椭圆的定义,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 和双曲线
和双曲线 有相同的焦点
有相同的焦点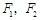 ,点
,点 是两条曲线的一个交点,则
是两条曲线的一个交点,则 的值为 .
的值为 . 和双曲线
和双曲线 有相同的焦点
有相同的焦点 、
、 ,P是两曲线的一个公共点,则
,P是两曲线的一个公共点,则 的值是( )
的值是( )
 D.
D.
 和双曲线
和双曲线 有相同的焦点
有相同的焦点 是椭圆与双曲线的一个交点,则
是椭圆与双曲线的一个交点,则 等于: ( )
等于: ( )
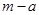 B.
B. C.
C. D.
D.
 和双曲线
和双曲线 有相同的左、右焦点
有相同的左、右焦点 ,P是两条曲线的一个交点,则
,P是两条曲线的一个交点,则 的值是( ).
的值是( ). B.
B.
 D.
D.