题目内容
若椭圆 和双曲线
和双曲线 有相同的焦点
有相同的焦点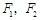 ,点
,点 是两条曲线的一个交点,则
是两条曲线的一个交点,则 的值为 .
的值为 .
【答案】

【解析】
试题分析:因为椭圆 和双曲线
和双曲线 有相同的焦点
有相同的焦点 ,点
,点 是两条曲线的一个交点,所以由椭圆、双曲线定义得到
是两条曲线的一个交点,所以由椭圆、双曲线定义得到 ,
, =
=  ,两式两边分别平方并相减得
,两式两边分别平方并相减得 。
。
考点:本题考查圆锥曲线的共同特征,考查了椭圆与双曲线的定义。
点评:解决本题的关键是根据所得出的条件灵活变形,根据椭圆和双曲线的定义, ,
, =
=  ,两式两边分别平方并相减得整理得到结论
,两式两边分别平方并相减得整理得到结论 。
。

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 和双曲线
和双曲线 有相同的焦点
有相同的焦点 、
、 ,P是两曲线的一个公共点,则
,P是两曲线的一个公共点,则 的值是( )
的值是( )
 D.
D.
 和双曲线
和双曲线 有相同的焦点
有相同的焦点 是椭圆与双曲线的一个交点,则
是椭圆与双曲线的一个交点,则 等于: ( )
等于: ( )
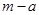 B.
B. C.
C. D.
D.
 和双曲线
和双曲线 有相同的左、右焦点
有相同的左、右焦点 ,P是两条曲线的一个交点,则
,P是两条曲线的一个交点,则 的值是( ).
的值是( ). B.
B.
 D.
D.