题目内容
已知函数 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若φ∈[0,π],则φ=
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若φ∈[0,π],则φ=
- A.

- B.

- C.

- D.

B
分析:由已知中函数 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同,我们可得两个函数的周期相同,进而求出ω值,得到函数f(x)的解析式,根据正弦型函数的对称性,我们可以确定出对称轴的方程,结合余弦函数的对称性,我也可得到函数g(x)的对称轴方程,由此即可求出φ值.
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同,我们可得两个函数的周期相同,进而求出ω值,得到函数f(x)的解析式,根据正弦型函数的对称性,我们可以确定出对称轴的方程,结合余弦函数的对称性,我也可得到函数g(x)的对称轴方程,由此即可求出φ值.
解答:∵函数 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.
∴两个函数的周期相同
故ω=2
则函数f(x)的对称轴为x=kπ+ ,k∈Z
,k∈Z
又∵g(x)的对称轴为x=kπ- ,k∈Z
,k∈Z
解得φ=
故选B
点评:本题考查的知识点是正弦型函数的对称性和余弦型函数的对称性,其中根据两个函数的对称轴完全相同,判断出两个函数的周期一致,进而求出ω值,得到对称轴的方程是解答本题的关键.
分析:由已知中函数
 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同,我们可得两个函数的周期相同,进而求出ω值,得到函数f(x)的解析式,根据正弦型函数的对称性,我们可以确定出对称轴的方程,结合余弦函数的对称性,我也可得到函数g(x)的对称轴方程,由此即可求出φ值.
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同,我们可得两个函数的周期相同,进而求出ω值,得到函数f(x)的解析式,根据正弦型函数的对称性,我们可以确定出对称轴的方程,结合余弦函数的对称性,我也可得到函数g(x)的对称轴方程,由此即可求出φ值.解答:∵函数
 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.∴两个函数的周期相同
故ω=2
则函数f(x)的对称轴为x=kπ+
 ,k∈Z
,k∈Z又∵g(x)的对称轴为x=kπ-
 ,k∈Z
,k∈Z解得φ=

故选B
点评:本题考查的知识点是正弦型函数的对称性和余弦型函数的对称性,其中根据两个函数的对称轴完全相同,判断出两个函数的周期一致,进而求出ω值,得到对称轴的方程是解答本题的关键.

练习册系列答案
相关题目
 和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同.若
和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同.若 ,则f(x)的取值范围是 .
,则f(x)的取值范围是 .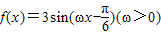 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若φ∈[0,π],则φ=( )
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若φ∈[0,π],则φ=( )
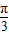
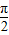
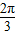
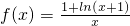 和g(x)=x-1-ln(x+1)
和g(x)=x-1-ln(x+1)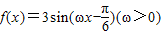 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若 ,则f(x)的取值范围是 .
,则f(x)的取值范围是 . 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若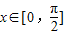 ,则f(x)的取值范围是 .
,则f(x)的取值范围是 .