题目内容
已知函数 和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同.若
和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同.若 ,则f(x)的取值范围是 .
,则f(x)的取值范围是 .
【答案】分析:由题意可得可得这2个函数的周期相同,故ω=2,故函数f(x)=2sin(2x- )+1.再由
)+1.再由 ,利用正弦函数的定义域和值域求得f(x)的范围.
,利用正弦函数的定义域和值域求得f(x)的范围.
解答:解:由 函数 和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同,可得这2个函数的周期相同,
和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同,可得这2个函数的周期相同,
故ω=2,故函数f(x)=2sin(2x- )+1.
)+1.
再由 ,可得
,可得 ,-1≤sin(2x-
,-1≤sin(2x- )≤1,∴-1≤f(x)≤3,
)≤1,∴-1≤f(x)≤3,
故答案为[-1,3].
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的对称性的应用,正弦函数的定义域和值域,属于中档题.
 )+1.再由
)+1.再由 ,利用正弦函数的定义域和值域求得f(x)的范围.
,利用正弦函数的定义域和值域求得f(x)的范围.解答:解:由 函数
 和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同,可得这2个函数的周期相同,
和g(x)=3cos(2x+φ)+1的图象的对称中心完全相同,可得这2个函数的周期相同,故ω=2,故函数f(x)=2sin(2x-
 )+1.
)+1.再由
 ,可得
,可得 ,-1≤sin(2x-
,-1≤sin(2x- )≤1,∴-1≤f(x)≤3,
)≤1,∴-1≤f(x)≤3,故答案为[-1,3].
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的对称性的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
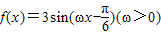 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若φ∈[0,π],则φ=( )
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若φ∈[0,π],则φ=( )
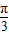
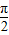
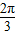
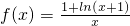 和g(x)=x-1-ln(x+1)
和g(x)=x-1-ln(x+1)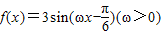 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若 ,则f(x)的取值范围是 .
,则f(x)的取值范围是 . 和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若
和g(x)=2cos(2x+φ)+1的图象的对称轴完全相同.若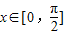 ,则f(x)的取值范围是 .
,则f(x)的取值范围是 .