题目内容
设函数f(t)对任意的整数x、y,均有f(x+y)=f(x)+f(y)+2xy,且f(1)=1.(I)当t∈Z时,用t的代数式表示g(t)=f(t+1)-f(t);
(II)当t∈Z时,求函数f(t)的解析式;
(Ⅲ)如果x∈[-1,1],a∈R,且
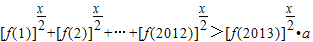 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】分析:(I)对抽象函数所满足的关系式,进行赋值,分别令x=t,y=1,代入化简即可得到结论;
(II)由(I)知 ,分别令t=1,2,3,…,得出t-1个式子,将这t-1个式子相加后化简即可得到函数f(t)的解析式;
,分别令t=1,2,3,…,得出t-1个式子,将这t-1个式子相加后化简即可得到函数f(t)的解析式;
(III)由(II)可知 ,从而不等式
,从而不等式 ,可转化为1+2x+3x+4x+…+2012x>2013x•a,也即
,可转化为1+2x+3x+4x+…+2012x>2013x•a,也即 最后利用而函数的单调性转化为恒成立问题即可求出实数a的取值范围.
最后利用而函数的单调性转化为恒成立问题即可求出实数a的取值范围.
解答:解:(I)由题设可令x=t,y=1,得f(t+1)=f(t)+f(1)+2t
∵f(1)=1
∴f(t+1)=f(t)+1+2t
∴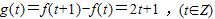 …(3分)
…(3分)
(II)由(I)知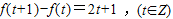
∴f(2)-f(1)=2×1+1,
f(3)-f(2)=2×2+1,
f(4)-f(3)=2×3+1,
…,

∴f(t)-f(1)=2[1+2+3+…+(t+1)]+(t-1)=t2-1
∴当t∈Z时,函数f(t)的解析式为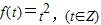 …(7分).
…(7分).
(III)由(II)可知 ,
,
所以不等式 ,
,
可转化为1+2x+3x+4x+…+2012x>2013x•a
也即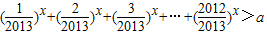 …(9分)
…(9分)
而函数 在x∈[-1,1]上单调减,
在x∈[-1,1]上单调减,
所以要使x∈[-1,1],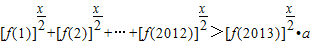 恒成立,
恒成立,
则有a<g(x)min,
而 ,
,
∴实数a的取值范围为(-∞,1006)…(12分).
点评:本题考查抽象函数的求值、计算与证明问题,抽象函数是相对于函数有具体解析式而言的,赋值法是解决抽象函数的一把“利剑”,本题属于中档题.
(II)由(I)知
 ,分别令t=1,2,3,…,得出t-1个式子,将这t-1个式子相加后化简即可得到函数f(t)的解析式;
,分别令t=1,2,3,…,得出t-1个式子,将这t-1个式子相加后化简即可得到函数f(t)的解析式;(III)由(II)可知
 ,从而不等式
,从而不等式 ,可转化为1+2x+3x+4x+…+2012x>2013x•a,也即
,可转化为1+2x+3x+4x+…+2012x>2013x•a,也即 最后利用而函数的单调性转化为恒成立问题即可求出实数a的取值范围.
最后利用而函数的单调性转化为恒成立问题即可求出实数a的取值范围.解答:解:(I)由题设可令x=t,y=1,得f(t+1)=f(t)+f(1)+2t
∵f(1)=1
∴f(t+1)=f(t)+1+2t
∴
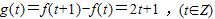 …(3分)
…(3分)(II)由(I)知
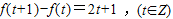
∴f(2)-f(1)=2×1+1,
f(3)-f(2)=2×2+1,
f(4)-f(3)=2×3+1,
…,

∴f(t)-f(1)=2[1+2+3+…+(t+1)]+(t-1)=t2-1
∴当t∈Z时,函数f(t)的解析式为
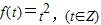 …(7分).
…(7分).(III)由(II)可知
 ,
,所以不等式
 ,
,可转化为1+2x+3x+4x+…+2012x>2013x•a
也即
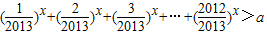 …(9分)
…(9分)而函数
 在x∈[-1,1]上单调减,
在x∈[-1,1]上单调减,所以要使x∈[-1,1],
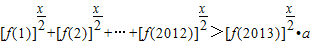 恒成立,
恒成立,则有a<g(x)min,
而
 ,
,∴实数a的取值范围为(-∞,1006)…(12分).
点评:本题考查抽象函数的求值、计算与证明问题,抽象函数是相对于函数有具体解析式而言的,赋值法是解决抽象函数的一把“利剑”,本题属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目