Question

设Sn为数列{an}的前n项和,已知a1≠0,2an-a1=S1·Sn,n∈N*.

(1)求a1,a2,并求数列{an}的通项公式;

(2)求数列{nan}的前n项和.

 

Answer 1

【答案】

(1) a1=1 a2=2 an=2n-1 (2) Bn=1+(n-1)·2n

【解析】

解:(1)令n=1,得2a1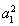-a1=,即a1=.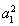

因为a1≠0,所以a1=1.

令n=2,得2a2-1=S2=1+a2,解得a2=2.

当n≥2时,由2an-1=Sn,2an-1-1=Sn-1两式相减,

得2an-2an-1=an,即an=2an-1.

于是数列{an}是首项为1,公比为2的等比数列.

因此,an=2n-1.所以数列{an}的通项公式为an=2n-1.

(2)由(1)知,nan=n·2n-1.

记数列{n·2n-1}的前n项和为Bn,

于是Bn=1+2×2+3×22+…+n×2n-1,①

2Bn=1×2+2×22+3×23+…+n×2n.②

①-②,得-Bn=1+2+22+…+2n-1-n·2n=2n-1-n·2n.

从而Bn=1+(n-1)·2n.