题目内容
已知双曲线 -
- =1(a>b,b>0)的离心率为
=1(a>b,b>0)的离心率为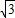 ,则椭圆
,则椭圆 +
+ =1的离心率为( )
=1的离心率为( )A.

B.

C.

D.

【答案】分析:先由题设条件求出双曲线的a,c的关系,从而得到a和 b的关系,再利用椭圆 +
+ =1的a和b关系求出椭圆的离心率.
=1的a和b关系求出椭圆的离心率.
解答:解:由题设条件可知双曲线的离心率为 ,
,
∴不妨设a=1.c= ,∴b=
,∴b=
∴椭圆 +
+ =1的a=1.b=
=1的a=1.b=
∴c=1
则椭圆 +
+ =1的离心率为e=
=1的离心率为e= .
.
故选D.
点评:本题考查椭圆、双曲线的标准方程及简单性质.本题是双曲线的椭圆的综合题,难度不大,只要熟练掌握圆锥曲线的性质就行.
 +
+ =1的a和b关系求出椭圆的离心率.
=1的a和b关系求出椭圆的离心率.解答:解:由题设条件可知双曲线的离心率为
 ,
,∴不妨设a=1.c=
 ,∴b=
,∴b=
∴椭圆
 +
+ =1的a=1.b=
=1的a=1.b=
∴c=1
则椭圆
 +
+ =1的离心率为e=
=1的离心率为e= .
.故选D.
点评:本题考查椭圆、双曲线的标准方程及简单性质.本题是双曲线的椭圆的综合题,难度不大,只要熟练掌握圆锥曲线的性质就行.

练习册系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为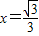 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
. =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为
,右准线方程为 .
.