题目内容

（2012•虹口区二模）已知椭圆
x2
t2
+
y2
5t
=1的焦点为（0，±
6
），则实数t=
2，3
2，3
．
分析：根据椭圆的焦点，确定椭圆的几何量的关系，即可求得实数t的值．
解答：解：根据题意，a2=5t，b2=t2
∴c2=a2-b2
∵椭圆
x2
t2
+
y2
5t
=1的焦点为（0，±
6
），
∴5t-t2=6
∴t2-5t+6=0
∴t=2，或3
故答案为：2，或3
点评：本题考查椭圆的几何性质与帮助方程，利用焦点确定几何量之间的关系是关键．
练习册系列答案
相关题目
（2012•虹口区二模）已知：函数g（x）=ax2-2ax+1+b（a≠0，b＜1），在区间
2，3
上有最大值4，最小值1，设函数f(x)=
g(x)
x
．
（1）求a、b的值及函数f（x）的解析式；
（2）若不等式f（2x）-k•2x≥0在x∈
-1，1
时恒成立，求实数k的取值范围．
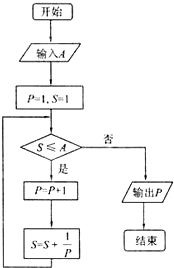（2012•虹口区二模）执行如图所示的程序框图，若输入A的值为2，则输出P的值为
4
4
．
（2012•虹口区二模）a，b∈R，a＞b且ab=1，则
a2+b2
a-b
的最小值等于
2
2
2
2
．
（2012•虹口区二模）函数f(x)=
x2+4x x≥0
4x-x2 x＜0
，则不等式f（2-x2）＞f（x）的解集是
（-2，1）
（-2，1）
．
（2012•虹口区二模）若非零向量
a
、
b
，满足|
a
|=|
b
|，且(2
a
+
b
)•
b
=0，则
a
与
b
的夹角大小为
120°
120°
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网