题目内容

已知f′（x）g（x）-f（x）g′（x）=x²（1-x），则函数 $数学公式$

A.
有极大值点1，极小值点0
B.
有极大值点0，极小值点1
C.
有极大值点1，无极小值点
D.
有极小值点0，无极大值点

C
分析：构造函数F（x）= $\text{[math]}$ ，则由商的导数，可得当x＜0时，F^′（x）＞0，0＜x＜1时，F^′（x）＞0，x＞1时，F^′（x）＜0，由极值的定义可知，在左右两侧的单调性相反，即左右两侧导数值异号的才为极值点．
解答：构造函数F（x）= $\text{[math]}$ ，则由商的导数，可得F^′（x）= $\text{[math]}$ = $\text{[math]}$
令F^′（x）=0，即 $\text{[math]}$ =0，解得，x=0，或x=1．
并且当x＜0时，F^′（x）＞0，0＜x＜1时，F^′（x）＞0，由极值的定义可知，即x=0不是函数F（x）的极值点；
同理，可得当x＞1时，F^′（x）＜0，由极值的定义可知，x=1是函数F（x）的极大值点．
故选C
点评：本题为极值点的判断，需构造函数，利用商的导数，结合极值的定义可得答案，属中档题．

练习册系列答案

随堂同步练习系列答案

数学奥赛天天练系列答案

数学口算每天一练系列答案

小学毕业生总复习系列答案

天天向上素质教育读本教材新解系列答案

完美学案系列答案

字词句篇与达标训练系列答案

名师面对面同步作业本系列答案

全品小学阅读系列答案

专项训练卷系列答案

相关题目

已知f（x）=（x-1）²，g（x）=4x-4数列{a_n}满足a₁=2，（a_n+1-a_n）g（a_n）+f（a_n）=0，（n∈N⁺）
（1）证明数列{a_n-1}是等比数列；
（2）设b_n=7f（a_n）-g（a_n+1），求数列{b_n}的前n项和S_n；
（3）在（2）的条件下，是否存在自然数M使得S_n＜M＜f（x）-g（x）+

对任意n∈N^*和任意实数x均成立，若存在求出满足条件的所有自然数M．

给出下列四个命题：
①已知f(x)+2f(

)=3x，则函数g（x）=f（2^x）在（0，1）上有唯一零点；
②对于函数f(x)=x

的定义域中任意的x₁、x₂（x₁≠x₂）必有f(

；
③已知f（x）=|2^-x+1-1|，a＜b，f（a）＜f（b），则必有0＜f（b）＜1；
④已知f（x）、g（x）是定义在R上的两个函数，对任意x、y∈R满足关系式f（x+y）+f（x-y）=2f（x）•g（y），且f（0）=0，但x≠0时f（x）•g（x）≠0．则函数f（x）、g（x）都是奇函数．
其中正确命题的序号是

已知f（x）=2^x，g（x）=3^x．
（1）当x为何值时，f（x）=g（x）？
（2）当x为何值时，f（x）＞1？f（x）=1？f（x）＜1？
（3）当x为何值时，g（x）＞3？g（x）=3？g（x）＜3？

已知函数f（x）=x²-alnx，x∈（1，2），
（1）判断函数f（x）的单调性；
（2）若f（x）在（1，2）为增函数，g(x)=x-a

在（0，1）上为减函数．
求证：方程f（x）=g（x）+2在（0，+∞）内有唯一解；
（3）当b＞-1时，若f(x)≥2bx-

在x∈（0，1）内恒成立，求实数b的取值范围．

已知f（x）=（x-1）²，g（x）=4x-4数列{a_n}满足a₁=2，（a_n+1-a_n）g（a_n）+f（a_n）=0，（n∈N⁺）
（1）证明数列{a_n-1}是等比数列；
（2）设b_n=7f（a_n）-g（a_n+1），求数列{b_n}的前n项和S_n；
（3）在（2）的条件下，是否存在自然数M使得S_n＜M＜f（x）-g（x）+

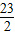对任意n∈N^*和任意实数x均成立，若存在求出满足条件的所有自然数M．