题目内容
(1)若函数f(x)=x2+2(a-1)x+2在区间(-∞,4］上是减函数，求实数a的取值范围；(2)y=kx2-
x+1在［0,+∞)上单调递减，求实数k的取值范围.
思路分析：(1)二次函数的单调区间依赖于其对称轴的位置，处理二次函数的单调性问题需对对称轴进行讨论.(2)y=kx2-
x+1中的k是否为零要注意讨论.
解：(1)f(x)=x2+2(a-1)x+2，其对称轴为x=
=1-a，若要二次函数在(-∞,4］上单调递减，必须满足1-a≥4,即a≤-3.如图所示.
(2)k=0时，y=-
x+1满足题意；k＞0时，抛物线开口向上，在［0,+∞)上不可能单调递减；k＜0时，对称轴x=
＜0在［0,+∞）上单调递减.
综上，k≤0.
练习册系列答案
相关题目
( n Î N, n ³ 2).
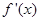满足0＜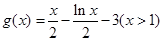
是否是集合M中的元素，并说明理由；
，
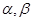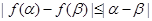
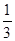x3+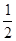
ax2+ax-2(a∈R),
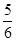，求实数a的取值范围.