题目内容
已知函数 ,
, .
.
(1)求 的单调区间;
的单调区间;
(2)当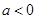 时,若对于任意的
时,若对于任意的 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
(1)当 时函数
时函数 在
在 上单调递减,在
上单调递减,在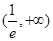 上单调递增;当
上单调递增;当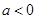 时函数
时函数 在
在 上单调递增,在
上单调递增,在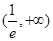 上单调递减。(2)
上单调递减。(2)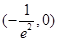
解析试题分析:(1)先求导可得 ,讨论导数再其定义域
,讨论导数再其定义域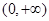 内的正负,导数正得增区间,导数负得减区间。讨论导数符号问题时应注意对
内的正负,导数正得增区间,导数负得减区间。讨论导数符号问题时应注意对 正负的讨论。(2)将问题转化为当
正负的讨论。(2)将问题转化为当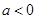 时,对于任意的
时,对于任意的
 恒成立。令
恒成立。令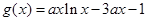 ,先求导,再讨论导数的正负,从而得函数
,先求导,再讨论导数的正负,从而得函数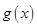 的单调性,根据单调性求函数
的单调性,根据单调性求函数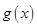 的最值,使其最小值大于等于0即可。
的最值,使其最小值大于等于0即可。
解:(1)函数 的定义域为
的定义域为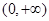 . 1分
. 1分
因为 , 2分
, 2分
令 ,解得
,解得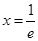 . 3分
. 3分
当 时, 随着
时, 随着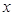 变化时,
变化时, 和
和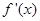 的变化情况如下:
的变化情况如下:
即函数 在
在 上单调递减,在
上单调递减,在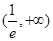 上单调递增. 5分
上单调递增. 5分
当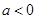 时, 随着
时, 随着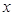 变化时,
变化时, 和
和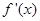 的变化情况如下:
的变化情况如下:
即函数 在
在 上单调递增,在
上单调递增,在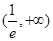 上单调递减. 7分
上单调递减. 7分
(2)当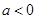 时,对于任意的
时,对于任意的 ,都有
,都有 成立,
成立,
即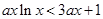 .
.
所以 .
.
设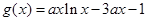 .
.
因为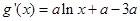
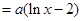 , 8分
, 8分
令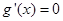 ,解得
,解得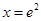 . 9分
. 9分
因为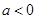 ,
,
所以随着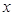 变化时,
变化时, 和
和 的变化情况如下:
的变化情况如下: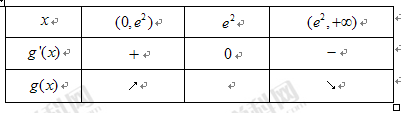
即函数 在
在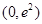 上单调递增,在
上单调递增,在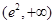 上单调递减. 10分
上单调递减. 10分
所以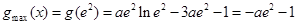 . 11分
. 11分
所以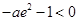 .
.
所以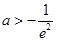 . 12分
. 12分
所以

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 (
( 的单位为:秒,
的单位为:秒, 的单位为:米/秒)的速度作变速直线运动,求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?
的单位为:米/秒)的速度作变速直线运动,求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?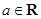 ,函数
,函数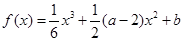 ,
,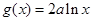 .
.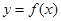 与曲线
与曲线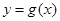 在它们的交点
在它们的交点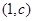 处的切线互相垂直,求
处的切线互相垂直,求 ,
,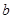 的值;
的值;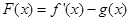 ,若对任意的
,若对任意的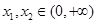 ,且
,且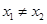 ,都有
,都有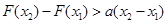 ,求
,求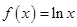 ,
,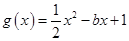 (
(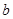 为常数).
为常数).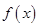 的图象在点
的图象在点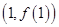 处的切线与函数
处的切线与函数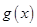 的图象相切,求实数
的图象相切,求实数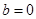 ,
,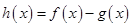 ,
,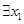 、
、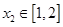 使得
使得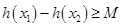 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;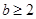 时,若对于区间
时,若对于区间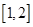 内的任意两个不相等的实数
内的任意两个不相等的实数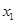 、
、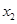 ,都有
,都有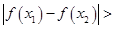
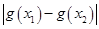 成立,求
成立,求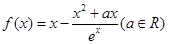 .
.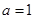 时,证明:当
时,证明:当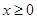 时,
时,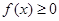 ;
;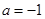 时,证明:
时,证明: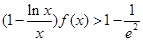 .
.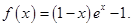
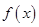 的最大值;
的最大值;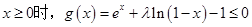 ,求
,求 的取值范围.
的取值范围.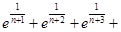 +
+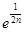
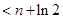 (n
(n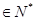 )
) 在点(1,0)处的切线.
在点(1,0)处的切线.