题目内容
已知球Ol、O2的半径分别为l、r,体积分别为V1、V2,表面积分别为S1、S2,当r∈(1,+∞)时,
的取值范围是
| V2-V1 |
| S2-S1 |
(
,+∞)
| 1 |
| 2 |
(
,+∞)
.| 1 |
| 2 |
分析:根据球的体积和表面积公式,代入
化简可得
[(r+1)+
-1],令t=r+1,由r∈(1,+∞)可得t∈(2,+∞),结合对勾函数的单调性,可得答案.
| V2-V1 |
| S2-S1 |
| 1 |
| 3 |
| 1 |
| r+1 |
解答:解:令
=
=
=
=
=
[(r+1)+
-1]
令t=r+1,由r∈(1,+∞)可得t∈(2,+∞)
∵y=t+
在(2,+∞)上单调递增,当t=2时t+
=
故
=
[(r+1)+
-1]>
(
-1)=
故
的取值范围是(
,+∞)
故答案为:(
,+∞)
| V2-V1 |
| S2-S1 |
| ||
| 4π(r2-1) |
| (r3-1) |
| 3(r2-1) |
| r2+r+1 |
| 3(r +1 ) |
| (r+1)2-(r+1)+1 |
| 3(r +1) |
| 1 |
| 3 |
| 1 |
| r+1 |
令t=r+1,由r∈(1,+∞)可得t∈(2,+∞)
∵y=t+
| 1 |
| t |
| 1 |
| t |
| 5 |
| 2 |
故
| V2-V1 |
| S2-S1 |
| 1 |
| 3 |
| 1 |
| r+1 |
| 1 |
| 3 |
| 5 |
| 2 |
| 1 |
| 2 |
故
| V2-V1 |
| S2-S1 |
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题以球的体积和表面积公式为载体考查了对勾函数的应用,对应函数是高中数学课本没有但用途很广的函数之一,特别是其单调性和极值一定要熟练掌握.

练习册系列答案
相关题目
 如图,已知圆柱体底面圆的半径为
如图,已知圆柱体底面圆的半径为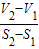 的取值范围是 .
的取值范围是 .