题目内容
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上且过点
轴上且过点 ,离心率是
,离心率是 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)直线 过点
过点 且与椭圆
且与椭圆 交于
交于 ,
, 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.
解:(Ⅰ)设椭圆 的方程为
的方程为
 .
.
由已知可得 ………………………………3分
………………………………3分
解得 ,
, .
.
故椭圆 的方程为
的方程为 .…………………………………………6分
.…………………………………………6分
(Ⅱ)由已知,若直线 的斜率不存在,则过点
的斜率不存在,则过点 的直线
的直线 的方程为
的方程为 ,
,
此时 ,显然
,显然 不成立.……………7分
不成立.……………7分
若直线 的斜率存在,则设直线
的斜率存在,则设直线 的方程为
的方程为 .
.
则
整理得 .………………………………9分
.………………………………9分
由
 .
.
设 .
.
故 ,①
,①  . ②…………………10分
. ②…………………10分
因为 ,即
,即 .③
.③
①②③联立解得 . ……………………13分
. ……………………13分
所以直线 的方程为
的方程为 和
和 .………14分
.………14分

练习册系列答案
相关题目
 的定义域为
的定义域为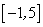 ,部分对应值如下表,
,部分对应值如下表, 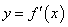 的图
的图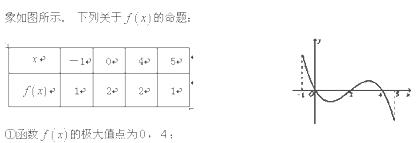
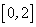 上是减函数;③如果当
上是减函数;③如果当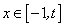 时,
时, 的最大值为4;
的最大值为4;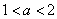 时,函数
时,函数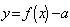 有
有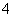 个零点;⑤函数
个零点;⑤函数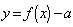 的零点个数可能为0、1、2、3、4个.其中正确命题的序号是
的零点个数可能为0、1、2、3、4个.其中正确命题的序号是  展开式中含
展开式中含 项的系数为 .
项的系数为 .
 -
- =1(a>0,b>0)的左、右焦点分别为F1(-c,0)、F2(c,0).若双曲线上存在点P,使
=1(a>0,b>0)的左、右焦点分别为F1(-c,0)、F2(c,0).若双曲线上存在点P,使 =
= ,则该双曲线的离心率的取值范围是________.
,则该双曲线的离心率的取值范围是________.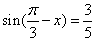 ,则
,则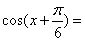
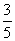 B.
B.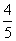 C.
C.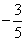 D.
D.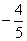
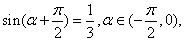 则
则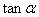 的值为________.
的值为________. 的展开式的常数项是(
的展开式的常数项是( )
)  的值域是( )
的值域是( ) B.
B.  C.
C.  D.
D. 