题目内容
已知函数 .
.
(1)求f(x)的定义域和值域;
(2)若 的值.
的值.
(3)若曲线f(x)在点P(x0,f(x0)) 处的切线平行直线
处的切线平行直线 ,求x0的值.
,求x0的值.
解(1) =
= (2分)
(2分)
由 ,
,
∴ (4分)
(4分)
则 (6分)
(6分)
(2)∵ ,∴
,∴ .
.
∴ (7分)
(7分)
∵ ,∴
,∴
∴ (8分)
(8分)
∴ =2sin(x+
=2sin(x+ )cos(x+
)cos(x+ )=
)= (10分)
(10分)
(3)f/(x)=cosx-sinx
由题意得 =
= (12分)
(12分)
∴ 又∵
又∵
∴ (14分)
(14分)
分析:(1)根据分式有意义的条件可得,cosx≠0,求解即可得函数的定义域;利用二倍角公式及辅助角对函数化简可得f(x)= ,结合正弦函数性质可求函数的值域,
,结合正弦函数性质可求函数的值域,
(2)由于cos2x=sin(2x+ )=sin[2(x+
)=sin[2(x+ )],故需要求sin(x+
)],故需要求sin(x+ ),cos(x+
),cos(x+ ),
), 代入可求sin(x+
代入可求sin(x+ ),结合已知条件中 x的范围可求cos(x+
),结合已知条件中 x的范围可求cos(x+ ),然后代入可求,
),然后代入可求,
(3)对函数求导可得,f/(x)=cosx-sinx代入已知可得, =
=
从而可得 结合
结合 可求.
可求.
点评:本题主要考查了正弦函数的定义域及值域的求解,辅助角公式的应用,导数的基本运算,及由三角函数值求解角等知识的综合运用.
 =
= (2分)
(2分)由
 ,
,∴
 (4分)
(4分)则
 (6分)
(6分)(2)∵
 ,∴
,∴ .
.∴
 (7分)
(7分)∵
 ,∴
,∴
∴
 (8分)
(8分)∴
 =2sin(x+
=2sin(x+ )cos(x+
)cos(x+ )=
)= (10分)
(10分)(3)f/(x)=cosx-sinx
由题意得
 =
= (12分)
(12分)∴
 又∵
又∵
∴
 (14分)
(14分)分析:(1)根据分式有意义的条件可得,cosx≠0,求解即可得函数的定义域;利用二倍角公式及辅助角对函数化简可得f(x)=
 ,结合正弦函数性质可求函数的值域,
,结合正弦函数性质可求函数的值域,(2)由于cos2x=sin(2x+
 )=sin[2(x+
)=sin[2(x+ )],故需要求sin(x+
)],故需要求sin(x+ ),cos(x+
),cos(x+ ),
), 代入可求sin(x+
代入可求sin(x+ ),结合已知条件中 x的范围可求cos(x+
),结合已知条件中 x的范围可求cos(x+ ),然后代入可求,
),然后代入可求,(3)对函数求导可得,f/(x)=cosx-sinx代入已知可得,
 =
=
从而可得
 结合
结合 可求.
可求.点评:本题主要考查了正弦函数的定义域及值域的求解,辅助角公式的应用,导数的基本运算,及由三角函数值求解角等知识的综合运用.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.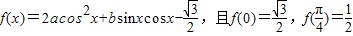 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.