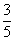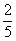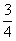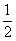题目内容
从{1,2,3,4,5}中随机选取一个数为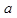 ,从{1,2,3}中随机选取一个数为
,从{1,2,3}中随机选取一个数为 ,则
,则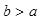 的概率是( )
的概率是( )
A. | B.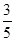 | C. | D. |
D
解析试题分析:由题意知本题是一个古典概型,试验包含的所有事件根据分步计数原理知共有5×3种结果,而满足条件的事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果解:由题意知本题是一个古典概型,∵试验包含的所有事件根据分步计数原理知共有5×3种结果,而满足条件的事件是a=1,b=2;a=1,b=3;a=2,b=3共有3种结果,∴由古典概型公式得到P= 故选D.
故选D.
考点:古典概型
点评:本题考查离散型随机变量的概率问题,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列各组事件中,不是互斥事件的是 ( )
| A.一个射手进行一次射击,命中环数大于8与命中环数小于6 |
| B.播种菜籽100粒,发芽90粒与发芽80粒 |
| C.检查某种产品,合格率高于70%与合格率为70% |
| D.统计一个班数学期中考试成绩,平均分数不低于90分与平均分数不高于120分 |
下列叙述错误的是( ).
A.若事件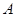 发生的概率为 发生的概率为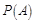 ,则 ,则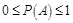 |
| B.互斥事件不一定是对立事件,但是对立事件一定是互斥事件 |
| C.5张奖券中有一张有奖,甲先抽,乙后抽,则乙与甲中奖的可能性相同 |
| D.某事件发生的概率是随着试验次数的变化而变化的 |
某5个同学进行投篮比赛,已知每个同学投篮命中率为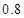 ,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记
,每个同学投篮2次,且投篮之间和同学之间都没有影响.现规定:投中两个得100分,投中一个得50分,一个未中得0分,记 为5个同学的得分总和,则
为5个同学的得分总和,则 的数学期望为( )
的数学期望为( )
| A.400 | B.200 | C.100 | D.80 |
已知函数: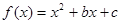 ,其中:
,其中: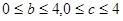 ,记函数
,记函数 满足条件:
满足条件: 为事件为A,则事件A发生的概率为 ( )
为事件为A,则事件A发生的概率为 ( )
A.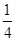 | B. | C.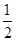 | D.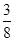 |
有五条线段长度分别为 ,从这
,从这 条线段中任取
条线段中任取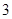 条,则所取
条,则所取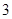 条线段能构成一个三角形的概率为
条线段能构成一个三角形的概率为
A. | B. | C. | D. |




 的分布列如图,设
的分布列如图,设 ,则( )
,则( )


 B、
B、
 D、
D、