题目内容
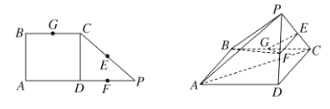
【题目】在平面直角坐标系![]() 中,如图放置的边长为
中,如图放置的边长为![]() 的正方形
的正方形![]() 沿
沿![]() 轴滚动(无滑动滚动),点
轴滚动(无滑动滚动),点![]() 恰好经过坐标原点,设顶点
恰好经过坐标原点,设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 的判断正确的是( )
的判断正确的是( )
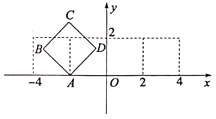
A.函数![]() 是奇函数B.对任意的
是奇函数B.对任意的![]() ,都有
,都有![]()
C.函数![]() 的值域为
的值域为![]() D.函数
D.函数![]() 在区间
在区间![]() 上单调递增
上单调递增
【答案】BCD
【解析】
根据正方形的运动,得到点![]() 的轨迹,作出对应函数图像,根据图像,即可得出结果.
的轨迹,作出对应函数图像,根据图像,即可得出结果.
由题意,当![]() 时,顶点
时,顶点![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 圆;
圆;
当![]() 时,顶点
时,顶点![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 圆;
圆;
当![]() 时,顶点
时,顶点![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 圆;
圆;
当![]() ,顶点
,顶点![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,以
为圆心,以![]() 为半径的
为半径的![]() 圆,与
圆,与![]() 的形状相同,因此函数
的形状相同,因此函数![]() 在
在![]() 恰好为一个周期的图像;
恰好为一个周期的图像;
所以函数![]() 的周期是
的周期是![]() ;
;
其图像如下:
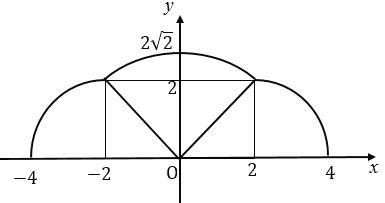
A选项,由图像及题意可得,该函数为偶函数,故A错;
B选项,因为函数的周期为![]() ,所以
,所以![]() ,因此
,因此![]() ;故B正确;
;故B正确;
C选项,由图像可得,该函数的值域为![]() ;故C正确;
;故C正确;
D选项,因为该函数是以![]() 为周期的函数,因此函数
为周期的函数,因此函数![]() 在区间
在区间![]() 的图像与在区间
的图像与在区间![]() 图像形状相同,因此,单调递增;故D正确;
图像形状相同,因此,单调递增;故D正确;
故选:BCD.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目