题目内容
已知椭圆C: ,一个顶点为A(0,2)
,一个顶点为A(0,2)
(1)若将椭圆C绕点P(1,2)旋转180°得到椭圆D,求椭圆D方程
(2)若椭圆C与直线y=kx+m (k≠0)相交于不同的M、N两点,且|AM|=|AN|,
求m的取值范围.
解:(1)由题意得,椭圆C的对称中心(0,0)关于点P(1,2)的对称点为(2,4),且对称轴平行于坐标轴,
长轴、短轴的长度不变,故将椭圆C绕点P(1,2)旋转180°得到椭圆D的方程为 +
+ =1.
=1.
(2) 设M(x1,y1)、N(x2,y2),∵|AM|=|AN|,∴A在线段MN的中垂线上.
把M(x1,y1)、N(x2,y2),代入椭圆C: 的方程得:
的方程得: +
+ =1,①
=1,①
 +
+ =1 ②,用①减去②得:
=1 ②,用①减去②得: =
= ,
,
∴k= =-
=- ×
× ,再由中垂线的性质得
,再由中垂线的性质得 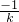 =
= =
= ,
,
∴ =
= ,∴y1+y2=-2,∴x1+x2=-3k(y1+y2)=-6k,
,∴y1+y2=-2,∴x1+x2=-3k(y1+y2)=-6k,
故MN的中点(-3k,-1),
把y=kx+m代入椭圆C: 得,(1+3k2)x2+6kmx+3m2-12=0,
得,(1+3k2)x2+6kmx+3m2-12=0,
∴x1+x2=-6k= ,∴m=1+3k2,∴mx2+6kmx+3m2-12=0,
,∴m=1+3k2,∴mx2+6kmx+3m2-12=0,
由题意知,判别式大于0,即 36k2m2-4m(3m2-12)>0,
36×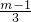 ×m2-12m3+48m>0,m(m-4)<0,∴0<m<4,
×m2-12m3+48m>0,m(m-4)<0,∴0<m<4,
故 m的取值范围为 (0,4).
分析:(1)椭圆C的对称中心(0,0)关于点P(1,2)的对称点为(2,4),且对称轴平行于坐标轴,长轴、短轴的长度不变.
(2)把M(x1,y1)、N(x2,y2),代入椭圆C相减,利用斜率公式及A在线段MN的中垂线上,求得y1+y2=-2,x1+x2=-6k,把y=kx+m代入椭圆C: 化为关于x的一元二次方程,再利用判别式大于0,求出m的取值范围.
化为关于x的一元二次方程,再利用判别式大于0,求出m的取值范围.
点评:本题考查利用对称法求椭圆的标准方程,斜率公式、中点公式的应用,以及一元二次方程有两个根的条件.
长轴、短轴的长度不变,故将椭圆C绕点P(1,2)旋转180°得到椭圆D的方程为
 +
+ =1.
=1.(2) 设M(x1,y1)、N(x2,y2),∵|AM|=|AN|,∴A在线段MN的中垂线上.
把M(x1,y1)、N(x2,y2),代入椭圆C:
 的方程得:
的方程得: +
+ =1,①
=1,① +
+ =1 ②,用①减去②得:
=1 ②,用①减去②得: =
= ,
,∴k=
 =-
=- ×
× ,再由中垂线的性质得
,再由中垂线的性质得 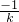 =
= =
= ,
,∴
 =
= ,∴y1+y2=-2,∴x1+x2=-3k(y1+y2)=-6k,
,∴y1+y2=-2,∴x1+x2=-3k(y1+y2)=-6k,故MN的中点(-3k,-1),
把y=kx+m代入椭圆C:
 得,(1+3k2)x2+6kmx+3m2-12=0,
得,(1+3k2)x2+6kmx+3m2-12=0,∴x1+x2=-6k=
 ,∴m=1+3k2,∴mx2+6kmx+3m2-12=0,
,∴m=1+3k2,∴mx2+6kmx+3m2-12=0,由题意知,判别式大于0,即 36k2m2-4m(3m2-12)>0,
36×
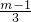 ×m2-12m3+48m>0,m(m-4)<0,∴0<m<4,
×m2-12m3+48m>0,m(m-4)<0,∴0<m<4,故 m的取值范围为 (0,4).
分析:(1)椭圆C的对称中心(0,0)关于点P(1,2)的对称点为(2,4),且对称轴平行于坐标轴,长轴、短轴的长度不变.
(2)把M(x1,y1)、N(x2,y2),代入椭圆C相减,利用斜率公式及A在线段MN的中垂线上,求得y1+y2=-2,x1+x2=-6k,把y=kx+m代入椭圆C:
 化为关于x的一元二次方程,再利用判别式大于0,求出m的取值范围.
化为关于x的一元二次方程,再利用判别式大于0,求出m的取值范围.点评:本题考查利用对称法求椭圆的标准方程,斜率公式、中点公式的应用,以及一元二次方程有两个根的条件.

练习册系列答案
相关题目
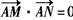 。
。 ,一个顶点为A(0,2)
,一个顶点为A(0,2)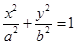
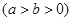 的一个顶点为A(2,0),离心率为
的一个顶点为A(2,0),离心率为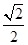 ,直线
,直线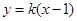 与椭圆C交于不同的两点M,N。
与椭圆C交于不同的两点M,N。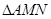 的面积为
的面积为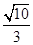 时,求k的值。
时,求k的值。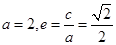 ∴
∴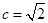 ∴
∴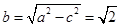 ∴
∴
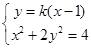
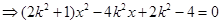
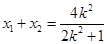 ,
,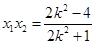

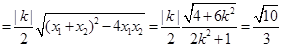
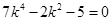 ,解得
,解得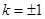
 ,一个顶点为A(0,2)。
,一个顶点为A(0,2)。