题目内容
设f(x)=2x3+ax2+bx+1的导数为f′(x),若函数y=f′(x)的图象关于直线x=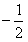 对称,且f′(1)=0,
对称,且f′(1)=0,
(Ⅰ)求实数a,b的值;
(Ⅱ)求函数f(x)的极值。
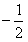 对称,且f′(1)=0,
对称,且f′(1)=0,(Ⅰ)求实数a,b的值;
(Ⅱ)求函数f(x)的极值。
解:(Ⅰ) ,
,
∵若函数y=f′(x)的图象关于直线x= 对称,且f′(1)=0,
对称,且f′(1)=0,
∴ 且
且 ,解得a=3,b=-12。
,解得a=3,b=-12。
(Ⅱ)由(Ⅰ)知 ,
,
 ,
,
f(x)的变化如下:

∴当x=-2时,f(x)取极大值,极大值为21;
当x=1时,f(x)取极小值,极小值为-6。
 ,
,∵若函数y=f′(x)的图象关于直线x=
 对称,且f′(1)=0,
对称,且f′(1)=0,∴
 且
且 ,解得a=3,b=-12。
,解得a=3,b=-12。(Ⅱ)由(Ⅰ)知
 ,
, ,
,f(x)的变化如下:

∴当x=-2时,f(x)取极大值,极大值为21;
当x=1时,f(x)取极小值,极小值为-6。

练习册系列答案
相关题目
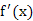 ,若函数
,若函数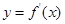 的图象关于直线
的图象关于直线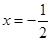 对称,且
对称,且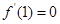 .](Ⅰ)求实数
.](Ⅰ)求实数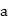 ,
,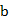 的值;(5分)(Ⅱ)求函数
的值;(5分)(Ⅱ)求函数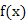 的极值
的极值