题目内容
一个多面体的直观图及三视图如图所示,其中M , N 分别是AF、BC 的中点,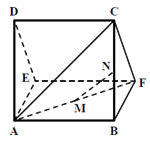
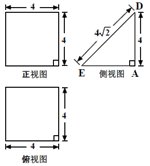
(1)求证:MN // 平面CDEF ;
(2)求二面角A-CF-B 的余弦值;
(1)详见解析;(2) .
.
解析试题分析:(1)由三视图知,该多面体是底面为直角三角形的直三棱柱ADE-BCF,且AB=BC=BF=4,DE=CF= ,∠CBF=90°,由此能证明MN∥平面CDEF.(2)(法一)作BQ⊥CF于Q,连结AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB为所求的二面角的平面角,由此能求出二面角A-CF-B的余弦值.
,∠CBF=90°,由此能证明MN∥平面CDEF.(2)(法一)作BQ⊥CF于Q,连结AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB为所求的二面角的平面角,由此能求出二面角A-CF-B的余弦值.
(2)(法二):以EA,AB,AD所在直线为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角A-CF-B的余弦值.
试题解析:解(1)证明:由三视图知,该多面体是底面为直角三角形的直三棱柱ADE-BCF,且AB=BC=BF=4,DE=CF= ,
,
,连结BE, M在BE上,连结CE
EM="BM,CN=BN," 所以 ∥
∥ ,所以
,所以 平面
平面
(2)方法一:作BQ⊥CF于Q,连结AQ,
面BFC⊥面ABFE,面ABFE∩面BFC=BF,
AB?面ABFE,AB⊥BF,
∴AB⊥面BCF,
CF?面BCF,∴AB⊥CF,BQ⊥CF,AB∩BQ=B,
∴CF⊥面ABQ,AQ?面ABQ,
AQ⊥CF,∴∠AQB为所求的二面角的平面角,(8分)
在Rt△ABQ中,tan∠AQB= ,
,
∴cos∠AQB= ,
,
∴二面角A-CF-B的余弦值为 .
.
(2)方法二:以EA,AB,AD所在直线为x轴,y轴,z轴建立空间直角坐标系,
所以
面CBF法向量为

设面ACF法向量为 ,
,
取 ,所以
,所以
设二面角 为
为 ,
,
考点:1.用空间向量求平面间的夹角;2.直线与平面平行的判定.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
已知 ,下列命题正确的是
,下列命题正确的是
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则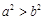 | D.若 ,则 ,则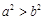 |


 侧棱与底面垂直,体积为
侧棱与底面垂直,体积为 ,高为
,高为 ,底面是正三角形,若
,底面是正三角形,若 是
是 中心,则
中心,则 与平面
与平面 所成的角大小是( )
所成的角大小是( )



 中,
中, 两两垂直,且均相等,
两两垂直,且均相等, 是
是 的中点,
的中点, 与
与 所成的角为( )
所成的角为( )
 的一条渐近线与圆
的一条渐近线与圆 相变于A.B两点,若
相变于A.B两点,若 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) C 3 D.4
C 3 D.4