题目内容
若函数y=x3-2mx2+m2x在x=1处取得极小值,则实数m=________.
1
分析:求导函数,利用f'(1)=0,求出m的值,再验证在1的左右附近,导数的符号,即可求得结论.
解答:由题意,求导函数可得f'(x)=(x-m)2+2x(x-m)
因为在x=1处取得极小值,所以f'(1)=0,即(1-m)2+2(1-m)=0
∴(1-m)(3-m)=0,∴m=1或m=3
①当m=1时,f'(x)=(x-1)2+2x(x-1)=(x-1)(3x-1),
若 <x<1时,f'(x)<0;若x>1时,f'(x)>0,此时在x=1处取得极小值,满足题意;
<x<1时,f'(x)<0;若x>1时,f'(x)>0,此时在x=1处取得极小值,满足题意;
②当m=3时,f'(x)=(x-3)2+2x(x-3)=(x-3)(3x-3),若x<1时,f'(x)>0,若1<x<3时,f'(x)<0,此时在x=1处取得极大值.不满足,舍去
综上:m=1
故答案为:1
点评:本题考查导数知识的运用,考查函数的极值,正确理解极值的含义是关键.
分析:求导函数,利用f'(1)=0,求出m的值,再验证在1的左右附近,导数的符号,即可求得结论.
解答:由题意,求导函数可得f'(x)=(x-m)2+2x(x-m)
因为在x=1处取得极小值,所以f'(1)=0,即(1-m)2+2(1-m)=0
∴(1-m)(3-m)=0,∴m=1或m=3
①当m=1时,f'(x)=(x-1)2+2x(x-1)=(x-1)(3x-1),
若
 <x<1时,f'(x)<0;若x>1时,f'(x)>0,此时在x=1处取得极小值,满足题意;
<x<1时,f'(x)<0;若x>1时,f'(x)>0,此时在x=1处取得极小值,满足题意;②当m=3时,f'(x)=(x-3)2+2x(x-3)=(x-3)(3x-3),若x<1时,f'(x)>0,若1<x<3时,f'(x)<0,此时在x=1处取得极大值.不满足,舍去
综上:m=1
故答案为:1
点评:本题考查导数知识的运用,考查函数的极值,正确理解极值的含义是关键.

练习册系列答案
相关题目
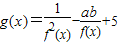 的定义域和值域均是[1,b],求实数a、b的值.
的定义域和值域均是[1,b],求实数a、b的值.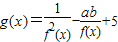 的定义域和值域均是[1,b],求实数a、b的值.
的定义域和值域均是[1,b],求实数a、b的值.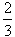 时有极值,求f(x)的单调区间;
时有极值,求f(x)的单调区间;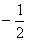 ,求实数m的值。
,求实数m的值。