题目内容
(1)若 =3,tan(α-β)=2,求tan(β-2α)的值;
=3,tan(α-β)=2,求tan(β-2α)的值;
(2)已知sin(3π+θ)= ,求
,求 +
+ .
.
解:(1)若 =3,则有
=3,则有  =3,解得 tanα=2.
=3,解得 tanα=2.
又tan(α-β)=2,∴tan(β-α)=-2,
∴tan(β-2α)=tan[(β-α)-α]= =
= =
= .
.
(2)∵已知sin(3π+θ)= =-sinθ,∴sinθ=-
=-sinθ,∴sinθ=- .
.
∴ +
+ =
= +
+
= +
+ =
= +
+ =
= =
=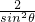 =18.
=18.
分析:(1)由条件利用同角三角函数的基本关系求得 tanα=2,由tan(α-β)=2 可得tan(β-α)=-2,再利用两角和差的正切公式求得tan(β-2α)=tan[(β-α)-α]的值.
(2)由sin(3π+θ)= =-sinθ,求得sinθ=-
=-sinθ,求得sinθ=- ,再利用诱导公式求得所求式子的值.
,再利用诱导公式求得所求式子的值.
点评:本题主要考查同角三角函数的基本关系,诱导公式、以及两角和差的正切公式的应用,属于中档题.
 =3,则有
=3,则有  =3,解得 tanα=2.
=3,解得 tanα=2.又tan(α-β)=2,∴tan(β-α)=-2,
∴tan(β-2α)=tan[(β-α)-α]=
 =
= =
= .
.(2)∵已知sin(3π+θ)=
 =-sinθ,∴sinθ=-
=-sinθ,∴sinθ=- .
.∴
 +
+ =
= +
+
=
 +
+ =
= +
+ =
= =
=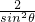 =18.
=18.分析:(1)由条件利用同角三角函数的基本关系求得 tanα=2,由tan(α-β)=2 可得tan(β-α)=-2,再利用两角和差的正切公式求得tan(β-2α)=tan[(β-α)-α]的值.
(2)由sin(3π+θ)=
 =-sinθ,求得sinθ=-
=-sinθ,求得sinθ=- ,再利用诱导公式求得所求式子的值.
,再利用诱导公式求得所求式子的值.点评:本题主要考查同角三角函数的基本关系,诱导公式、以及两角和差的正切公式的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
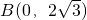 ,C(2cosθ,sinθ),其中
,C(2cosθ,sinθ),其中 .
.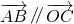 ,求tanθ的值;
,求tanθ的值;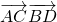 的最大值;
的最大值;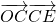 表示成θ的函数,记其最小值为f(a),求f(a)的表达式,并求f(a)的最大值.
表示成θ的函数,记其最小值为f(a),求f(a)的表达式,并求f(a)的最大值. =3,tan(α-β)=2,求tan(β-2α)的值;
=3,tan(α-β)=2,求tan(β-2α)的值; ,求
,求 +
+ .
.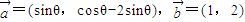 .
. ,求tanθ的值;
,求tanθ的值; ,求θ的值;
,求θ的值;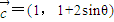 ,若
,若 ,求f(θ)的值域.
,求f(θ)的值域. =(sinθ,cosθ-2sinθ),
=(sinθ,cosθ-2sinθ), =(1,2),
=(1,2),  ,求tanθ的值;
,求tanθ的值;  (0<θ<π),求θ的值;
(0<θ<π),求θ的值; =(1,1+2sinθ),若f(θ)=
=(1,1+2sinθ),若f(θ)=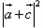 +sin2θ,求f(θ)的值域。
+sin2θ,求f(θ)的值域。