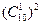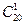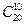题目内容
(本小题满分12分)
已知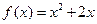 ,数列
,数列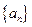 满足
满足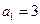 ,
,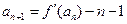 ,数列
,数列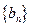 满足
满足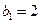 ,
,
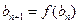 .
.
(1)求证:数列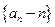 为等比数列.
为等比数列.
(2)令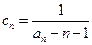 ,求证:
,求证: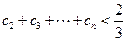 ;
;
(3)求证: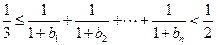
已知
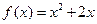 ,数列
,数列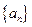 满足
满足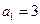 ,
,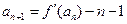 ,数列
,数列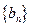 满足
满足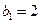 ,
,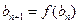 .
.(1)求证:数列
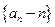 为等比数列.
为等比数列.(2)令
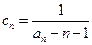 ,求证:
,求证: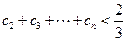 ;
;(3)求证:
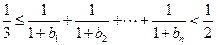
解析:(1)

设

 ,
,
 数列
数列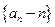 是首项为2,公比为2的等比数列,
是首项为2,公比为2的等比数列,

 (
( N*).
N*).
(2)


 .
.
(3)




又
 原式得证.
原式得证.


设


 ,
, 数列
数列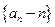 是首项为2,公比为2的等比数列,
是首项为2,公比为2的等比数列,
 (
( N*).
N*).(2)



 .
.(3)





又

 原式得证.
原式得证.略

练习册系列答案
相关题目
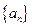 ,如果
,如果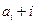 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数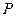 性质”。
性质”。 具有“
具有“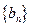 ,且
,且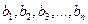 是
是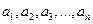 的一个排列
的一个排列 ;②数列
;②数列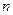 项和
项和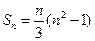 ,证明数列
,证明数列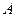 :1,2,3,…,
:1,2,3,…,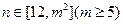 时,
时,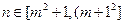 时,数
时,数 列
列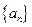 满足:
满足: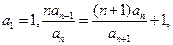 令
令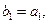
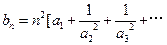
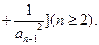
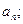
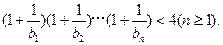
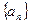 满足
满足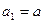 ,
,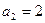 ,
,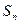 是数列的前
是数列的前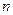 项和,且
项和,且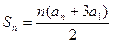 (
(
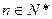 ).
).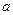 的值;
的值; 列
列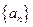 的通项公式;
的通项公式; (3)对于数列
(3)对于数列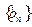 ,若存在常数M,使
,若存在常数M,使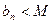 (
(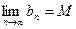 ,则M叫做数列
,则M叫做数列 (
(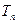 为数列
为数列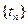 的前
的前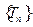 的上渐近值.
的上渐近值.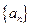 为等差数列,且
为等差数列,且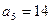 ,
, ,数列
,数列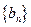 的前
的前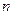 项和为
项和为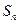 ,
,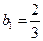 且
且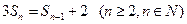 ;,
;,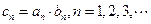 ,
,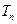 为数列
为数列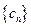 的前
的前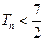 .
.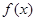 是定义在
是定义在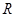 上恒不为零的函数,对任意的实数
上恒不为零的函数,对任意的实数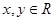 ,都有
,都有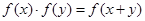 ,若
,若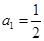 ,
,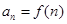 ,(
,(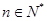 ),则数列
),则数列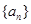 的前
的前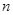 项和
项和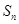 的最小值是( )
的最小值是( )
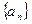 中,
中,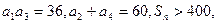 求
求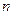 的范围.
的范围.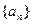 中,
中,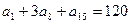 ,则
,则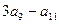 的值为多少?
的值为多少?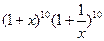 展开式中的常数项为
展开式中的常数项为