题目内容
(2013•唐山二模)已知动圆C经过点(0,1),且在x轴上截得弦长为2,记该圆圆心的轨迹为E.
(Ⅰ)求曲线E的方程;
(Ⅱ)过点M(0,
)的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为2
时,求直线m的方程.
(Ⅰ)求曲线E的方程;
(Ⅱ)过点M(0,
| 1 |
| 2 |
| 2 |
分析:(Ⅰ)设出动圆圆心坐标,由动圆C经过点(0,1)求出圆的半径,利用圆在x轴上截得弦长为2列式整理即可得到曲线E的方程;
(Ⅱ)设出直线m的方程,设出A,B两点的坐标,求导得到过A,B的抛物线的切线方程,利用抛物线定义求出AB长度,用点到直线距离公式求出C到AB的距离,写出面积后由面积等于2
求出直线的斜率,从而求得直线方程.
(Ⅱ)设出直线m的方程,设出A,B两点的坐标,求导得到过A,B的抛物线的切线方程,利用抛物线定义求出AB长度,用点到直线距离公式求出C到AB的距离,写出面积后由面积等于2
| 2 |
解答: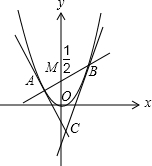 解:(Ⅰ)设圆C的圆心坐标为(x,y),则其半径r=
解:(Ⅰ)设圆C的圆心坐标为(x,y),则其半径r=
.
依题意,r2-y2=1,即x2+(y-1)2-y2=1,
整理得曲线E的方程为x2=2y.
(Ⅱ)如图,
设A(x1,y1),B(x2,y2),则y1=
x12,y2=
x22.
设直线m方程为y=kx+
,代入曲线E方程,得
x2-2kx-1=0,则x1+x2=2k,x1x2=-1.
对y=
x2求导,得y′=x.
于是过点A的切线为y=x1(x-x1)+
x12,即y=x1x-
x12 ①
同理得过点B的切线为y=x2x-
x22 ②
设C(x0,y0),由①、②及根与系数关系得
x0=
=k,y0=x1x0-
x12=-
.
M为抛物线的焦点,y=-
为抛物线的准线,由抛物线的定义,得
|AB|=y1+
+y2+
=k(x1+x2)+2=2(k2+1).
点C到直线m的距离d=
=
=
.
所以△ABC的面积S=
|AB|•d=(k2+1)
.
由已知(k2+1)
=2
,得k=±1.
故直线m的方程为y=±x+
.
 解:(Ⅰ)设圆C的圆心坐标为(x,y),则其半径r=
解:(Ⅰ)设圆C的圆心坐标为(x,y),则其半径r=| x2+(y-1)2 |
依题意,r2-y2=1,即x2+(y-1)2-y2=1,
整理得曲线E的方程为x2=2y.
(Ⅱ)如图,
设A(x1,y1),B(x2,y2),则y1=
| 1 |
| 2 |
| 1 |
| 2 |
设直线m方程为y=kx+
| 1 |
| 2 |
x2-2kx-1=0,则x1+x2=2k,x1x2=-1.
对y=
| 1 |
| 2 |
于是过点A的切线为y=x1(x-x1)+
| 1 |
| 2 |
| 1 |
| 2 |
同理得过点B的切线为y=x2x-
| 1 |
| 2 |
设C(x0,y0),由①、②及根与系数关系得
x0=
| x1+x2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
M为抛物线的焦点,y=-
| 1 |
| 2 |
|AB|=y1+
| 1 |
| 2 |
| 1 |
| 2 |
点C到直线m的距离d=
|kx0-y0+
| ||
|
|k2+
| ||||
|
| k2+1 |
所以△ABC的面积S=
| 1 |
| 2 |
| k2+1 |
由已知(k2+1)
| k2+1 |
| 2 |
故直线m的方程为y=±x+
| 1 |
| 2 |
点评:本题考查了椭圆的简单几何性质,考查了直线与圆锥曲线的关系,训练了利用导数求曲线上某点处的切线方程,考查了数学转化思想方法,解答此题的关键是利用抛物线的定义求解AB的长度,是难题.

练习册系列答案
相关题目