题目内容
三棱锥A-BCD的高AH=3| 3 |
分析：由题意画出图形，BC中点E，求出EH，斜高AE，再求EG，利用余弦定理求出GH．
解答：
解：由题意如图：H是底面△BCD的垂心，AB=AC，
所以E为BC的中点并且DE⊥BC，∠AEB=60°
∴EH=AHcot60°=3
a×
=3a
AE=6a G为△ABC的重心，EG=2a
由余弦定理可得GH=
=
a．
故答案为：
a．
解：由题意如图：H是底面△BCD的垂心，AB=AC，所以E为BC的中点并且DE⊥BC，∠AEB=60°
∴EH=AHcot60°=3
| 3 |
| ||
| 3 |
AE=6a G为△ABC的重心，EG=2a
由余弦定理可得GH=
| (2a)2+(3a)2-2×2a×3acos60° |
| 7 |
故答案为：
| 7 |
点评：本题考查棱锥的结构特征，二面角的问题，考查学生逻辑思维能力，是中档题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
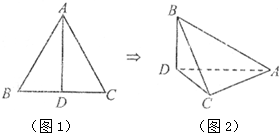已知正三角形ABC的边长为2，沿着BC边上的高AD将正三角形折起，使得平面ABD⊥平面ACD（如图），则三棱锥A-BCD的体积为
a,若AB=AC,二面角ABCD为60°,G为△ABC的重心,则HG之长为__________.
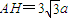，且H是底面△BCD的垂心，若AB=AC，二面角A-BC-D为60°，G为△ABC的重心，则HG的长为 ．