题目内容
已知F1,F2是椭圆的两个焦点,若椭圆上存在点P,使得PF1⊥PF2,则椭圆离心率的取值范围是( )
分析:先证明椭圆的短轴的一个端点是到椭圆的中心距离最短的点.若椭圆上存在点P,使得PF1⊥PF2,?c≥b,再利用a,b,c的关系,离心率计算公式即可得出.
解答:解:如图所示,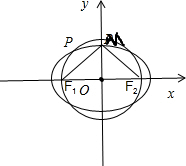
下面证明椭圆的短轴的一个端点是到椭圆的中心距离最短的点.
设椭圆上任意一点P(x0,y0),则
+
=1,可得
=b2(1-
).
∴|OP|2=
+
=
+b2(1-
)=
+b2≥b2,当且仅当x0=0时取等号.
∴椭圆的短轴的一个端点是到椭圆的中心距离最短的点.
若椭圆上存在点P,使得PF1⊥PF2,则c≥b,∴c2≥b2=a2-c2,化为e2≥
,解得e≥
.
又e<1,∴
≤e<1.
故选B.

下面证明椭圆的短轴的一个端点是到椭圆的中心距离最短的点.
设椭圆上任意一点P(x0,y0),则
| ||
| a2 |
| ||
| b2 |
| y | 2 0 |
| ||
| a2 |
∴|OP|2=
| x | 2 0 |
| y | 2 0 |
| x | 2 0 |
| ||
| a2 |
| c2 |
| a2 |
| x | 2 0 |
∴椭圆的短轴的一个端点是到椭圆的中心距离最短的点.
若椭圆上存在点P,使得PF1⊥PF2,则c≥b,∴c2≥b2=a2-c2,化为e2≥
| 1 |
| 2 |
| ||
| 2 |
又e<1,∴
| ||
| 2 |
故选B.
点评:本题考查了“椭圆的短轴的一个端点是到椭圆的中心距离最短的点”的性质、离心率计算公式等基础知识与基本技能方法,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目