题目内容
函数 的最大值为( )
的最大值为( )
A. | B. | C. | D.1 |
B
解析试题分析:可以利用单调性求解最值,也可以利用不等式的思想来求解最值。
因为
当x=1时取得等号。故选B.
考点:本试题考查了函数的最值运用。
点评:解决函数的最值问题,可以结合函数的单调性的性质来得到,也可以结合均值不等式的思想来求解得到,注意等号成立的条件即可,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数中,既是偶函数又在 单调递增的函数是( )
单调递增的函数是( )
A. | B. | C. | D. |
函数 的定义域为( )
的定义域为( )
A. | B.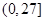 | C. | D. |
下列各组函数中表示同一函数的是 ( )
A.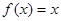 与 与 |
B. 与 与 |
C. 与 与 |
D. 与 与 |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D.  |
下列函数中,既是偶函数,又在区间 上单调递减的是( )
上单调递减的是( )
A. | B. | C.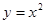 | D. |
函数 ( )
( )
A. | B. | C. | D. |
若 ,则函数
,则函数 的解集是( )
的解集是( )
A. | B. |
C. | D. |
设定义在实数集上函数 满足:
满足: ,且当
,且当 时,
时, ,则有( )
,则有( )
A.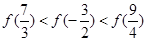 | B. |
C. | D. |