题目内容
平面直角坐标系xoy中,不等式x-1≤y≤
所表示的区域的面积为 .
| 1-x2 |
分析:先根据已知条件画出对应图象,分析出所求由哪几部分组成,再分别求出其面积,最后求和即可得到结论.
解答:解:根据已知条件可得其对应的平面区域如图:
由图得:所求为
的圆以及一等腰三角形的面积之和.
又因为:r=1,OA=OB=1,∠AOB=90°.
∴S=
r2+
×OB×OA•sin∠AOB=
π+
.
即所求平面区域的面积为:
+
.
故答案为:
+
.
由图得:所求为
| 3 |
| 4 |

又因为:r=1,OA=OB=1,∠AOB=90°.
∴S=
| 3π |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
即所求平面区域的面积为:
| 3π |
| 4 |
| 1 |
| 2 |
故答案为:
| 3π |
| 4 |
| 1 |
| 2 |
点评:本题主要考查线性规划的应用以及常见图形面积的求法.考查计算能力.解决问题的关键在于分析出所求区域由哪几部分组成.

练习册系列答案
相关题目
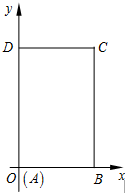 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.