题目内容
(本题满分12分)
设直线![]() ,双曲线
,双曲线![]() ,双曲线E的离心率为
,双曲线E的离心率为![]() 与E交于P、Q两点,直线l与y轴交于R点,且
与E交于P、Q两点,直线l与y轴交于R点,且![]()
(I)证明:![]()
(II)求双曲线E的方程;
(III)若点F是双曲线E的右焦点,M、N是双曲线上两点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:(I)![]() 双曲线离心率
双曲线离心率![]()
设直线l方程为![]() 由
由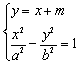 ,及
,及![]() 得
得![]() ①,
①,
设![]() ,则
,则![]() 是①的两根,
是①的两根,![]() ②.
②.
![]() 即
即![]()
![]() ③将②代入③得
③将②代入③得![]()
即![]() ④.得证
④.得证![]()
(II)易知![]()
![]() ,
,
将![]() 代入 ②得
代入 ②得![]() ⑤解④、⑤得
⑤解④、⑤得![]()
双曲线E的方程为![]()
(III)双曲线E的右焦点F为![]()
设![]() ,
,
![]() .
.
把M、N两点坐标代入![]() 得
得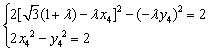
整理得![]() ,且
,且![]()
![]() ,得
,得![]() ,
,
因此所求![]() 的范围是
的范围是![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面