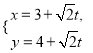题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)设函数![]() ,函数
,函数![]() 有且仅有一个零点.
有且仅有一个零点.
(i)求![]() 的值;
的值;
(ii)若![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
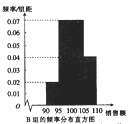
【答案】(1)![]() (2)(ⅰ)a=1(ⅱ)
(2)(ⅰ)a=1(ⅱ)![]()
【解析】试题分析:(1)当a=﹣1时,函数f(x)=(x2﹣2x)lnx+ax2+2=(x2﹣2x)lnx﹣x2+2,求出f′(x),则k=f′(1),代入直线方程的点斜式可得切线的方程.
(2)①令g(x)=f(x)﹣x﹣2=0,则(x2﹣2x)lnx+ax2+2=x+2,即![]() ,构造函数h(x)=
,构造函数h(x)=![]() ,确定h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,可得h(x)max=h(1)=1,即可求a的值;
,确定h(x)在(0,1)上单调递增,在(1,+∞)上单调递减,可得h(x)max=h(1)=1,即可求a的值;
②当a=1时,g(x)=(x2﹣2x)lnx+x2﹣x,若![]() ,g(x)≥m,只需g(x)min≥m.
,g(x)≥m,只需g(x)min≥m.
试题解析:
(1)当![]() 时,
时, ![]() ,
, ![]() ,
,
∴![]()
![]() ,又
,又![]()
∴![]() 在
在![]() 处的切线方程
处的切线方程![]() .
.
(2)(ⅰ)令![]() ,则
,则![]()
∴![]() 令
令![]() , 则
, 则![]() .
.
令![]() ,则
,则![]()
![]() ,
,
![]() ,
,![]() 在
在![]() 上是减函数 又
上是减函数 又![]() ,
,
∴当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
![]() ,∴当函数
,∴当函数![]() 有且只有一个零点时,
有且只有一个零点时, ![]() .
.
(ⅱ)当![]() ,
, ![]() ,若
,若![]() 时,
时, ![]() 恒成立,
恒成立,
只需![]()
![]() .令
.令![]() 得
得![]() 或
或![]() ,
,
![]() ,
, ![]() 函数
函数![]() 在
在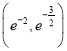 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又∵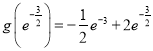 ,
, ![]()
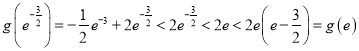 ,即
,即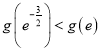 .
.
∴![]() ,
, ![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.