题目内容

若α∈(0，
π2
)，且cos2α=sin2α，则tanα=
 
．
分析：由α的范围得到cosα≠0，已知等式右边利用二倍角的正弦函数公式化简，再两边除以cosα，利用同角三角函数间的基本关系化简即可求出tanα的值．
解答：解：∵cos2α=sin2α=2sinαcosα，且α∈（0，
π
2
），即cosα≠0，
∴cosα=2sinα，
则tanα=
sinα
cosα
=
sinα
2sinα
=
1
2
．
故答案为：
1
2
点评：此题考查了二倍角的正弦函数公式，以及同角三角函数间的基本关系，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
已知函数f（x）=-3x-x3，x∈R，若θ∈[0，
π2
]时，不等式f（cos2θ-2t）+f（4sinθ-3）≥0恒成立，则实数t的取值范围是
 
．
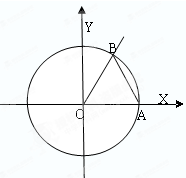如图，在平面直角坐标系xoy中，角α的始边与x轴的非负半轴重合且与单位圆相交于A点，它的终边与单位圆相交于x轴上方一点B，始边不动，终边在运动．
（1）若点B的横坐标为-
4
5
，求tanα的值；
（2）若△AOB为等边三角形，写出与角α终边相同的角β的集合；
（3）若α∈[0，
2π
3
]，请写出弓形AB的面积S与α的函数关系式，并指出函数的值域．
已知函数f（x）=（x2+1）e2x，若0°＜2α＜90°，90°＜β＜180°a=（sinα）cosβ，b=（cosα）sinβ，c=（cosα）cosβ，则f（a），f（b），f（c）的大小关系是（　　）
设f（x）=x3（x∈R），若0≤θ＜
π
2
时，f（m•sinθ）+f（2-m）＞0恒成立，则实数m的取值范围是（　　）
已知函数f(x)=2
3
sinxcosx-2cos2x+1．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）若α∈(0，
π
2
)，且f（α）=1，求α的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网