题目内容
已知函数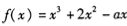 .对于任意实数x恒有
.对于任意实数x恒有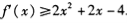
(1)求实数 的最大值;
的最大值;
(2)当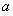 最大时,函数
最大时,函数 有三个零点,求实数k的取值范围。
有三个零点,求实数k的取值范围。
【答案】
(1)3;(2)
【解析】
试题分析:(1)根据函数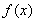 求出导函数,再根据所给的不等式,利用恒成立的条件求出实数
求出导函数,再根据所给的不等式,利用恒成立的条件求出实数 的范围,从而确定
的范围,从而确定 的最大值.
的最大值.
(2)由(1)可得 的值,从而根据函数
的值,从而根据函数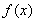 确定函数
确定函数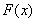 的解析式,由于函数
的解析式,由于函数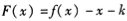 有三个零点,所以通过对函数
有三个零点,所以通过对函数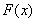 求导,了解函数
求导,了解函数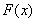 的图像的走向,以及对函数的极值的正负性作出规定,即可得到所需的结论.
的图像的走向,以及对函数的极值的正负性作出规定,即可得到所需的结论.
试题解析:(1)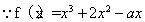
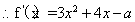 对于
对于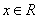 恒有
恒有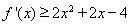 ,即
,即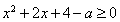 对于
对于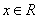 恒成立
恒成立
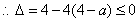
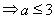
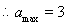
(2) 有三个零点
有三个零点
 有三个不同的实根
有三个不同的实根 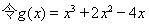 ,则
,则
令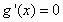 解得
解得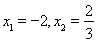
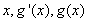 情况如下表:
情况如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| 单调递增 | 极大值8 | 单调递减 | 极小极 | 单调递增 |
由上表知,当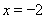 时
时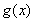 取得极大值
取得极大值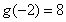 ,当
,当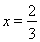 时
时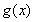 取得极小值
取得极小值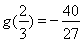
数形结合可知,实数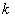 的取值范围为
的取值范围为 .
.
考点:1.函数的导数.2.函数的最值.3.函数的极值.4.函数与方程的关系.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目









 .则P点的轨迹一定通过△ABC的重心其中正确命题的序号为________
.则P点的轨迹一定通过△ABC的重心其中正确命题的序号为________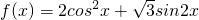 ,
,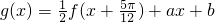 ,其中a,b为非零实常数.
,其中a,b为非零实常数.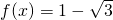 ,
,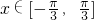 ,求x;
,求x;