题目内容
下列函数中,y的最小值等于4的是( )
A.y=
| B.y=2x+
| ||||||
| C.y=2x+4•2-x(x∈R) | D.y=
|
A:∵y=
=
=2(
+
)
令t=
,则t≥2,则函数y=
=2(t+
)单调递增,则y≥5,即最小值为5
B:∵在y=2x+
中,当x<0时,y<0,则函数的最小值不是4
C:y=2x+4•2-x=
+2x≥2
=4(当且仅当2x=
即x=1时取等号),即函数的最小值为4
D:y=sinx+
,令t=sinx∈(0,1],则y=t+
在(0,1]上单调递减,当t=1时函数有最小值5
故选C
| 2(x2+5) | ||
|
| 2(x2+4+1) | ||
|
| x2+4 |
| 1 | ||
|
令t=
| x2+4 |
| 2(x2+5) | ||
|
| 1 |
| t |
B:∵在y=2x+
| 2 |
| x |
C:y=2x+4•2-x=
| 4 |
| 2x |
|
| 4 |
| 2x |
D:y=sinx+
| 4 |
| sinx |
| 4 |
| t |
故选C

练习册系列答案
相关题目
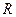 上的函数
上的函数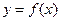 的值域为
的值域为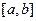 ,则函数
,则函数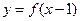 的值域为( )
的值域为( )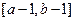 ;
;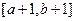 ;
;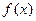 的定义域为[0,1],则函数
的定义域为[0,1],则函数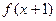 的定义域是
的定义域是 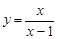 ,给出下列四个命题:①函数的图象关于点(1,1)对称;②函数的图象关于直线
,给出下列四个命题:①函数的图象关于点(1,1)对称;②函数的图象关于直线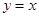 对称;③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数
对称;③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数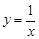 的图象重合。其中正确命题的序号是---------------。
的图象重合。其中正确命题的序号是---------------。 且
且 ,函数
,函数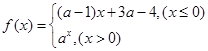 满足对任意实数
满足对任意实数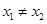 ,都有
,都有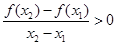 成立,则
成立,则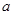 的取值范围是 ( )
的取值范围是 ( )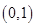
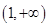

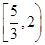
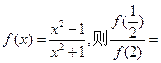 ( )
( )