题目内容
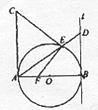
 如图,∠BAC=90°,直线l与以AB为直径的圆相切于点B,点E是圆上异于A、B的任意一点,直线AE与l相交于D点.
如图,∠BAC=90°,直线l与以AB为直径的圆相切于点B,点E是圆上异于A、B的任意一点,直线AE与l相交于D点.
(1)如果AD=10,AB=8,求DE的长;
(2)连接CE,过点E作CE的垂线交线段AB于点F,求证: .
.
(1)解:∵BD是切线,AD=10,AB=8
∴BD=6,
∵DB2=DE•DA
∴DE= =3.6;
=3.6;
(2)证明:连接BE,∵AB为圆的直径,∴∠AEB=90°
∴∠CEA=∠FEB
∵A,C,E,F四点共圆
∴∠C=∠EFB
∴△CEA∽△FEB
∴
∵△ABE∽△ABD
∴
∴
分析:(1)由于DB是圆的切线,因此根据切割线定理得出的DB2=DE•DA即可求出DE的长;
(2)连接BE,证明△CEA∽△FEB,ABE∽△ABD,即可得到结论.
点评:本题主要考查了切线的性质、切割线定理、圆周角定理、相似三角形的判定和性质等知识点,属于中档题.
∴BD=6,
∵DB2=DE•DA
∴DE=
 =3.6;
=3.6;(2)证明:连接BE,∵AB为圆的直径,∴∠AEB=90°

∴∠CEA=∠FEB
∵A,C,E,F四点共圆
∴∠C=∠EFB
∴△CEA∽△FEB
∴

∵△ABE∽△ABD
∴

∴

分析:(1)由于DB是圆的切线,因此根据切割线定理得出的DB2=DE•DA即可求出DE的长;
(2)连接BE,证明△CEA∽△FEB,ABE∽△ABD,即可得到结论.
点评:本题主要考查了切线的性质、切割线定理、圆周角定理、相似三角形的判定和性质等知识点,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 选修4-1:几何证明选讲
选修4-1:几何证明选讲
 选修4-1:几何证明选讲
选修4-1:几何证明选讲